这篇简单的谈谈后缀树原理及实现。
如前缀树原理一般,后缀trie树是将字符串的每个后缀使用trie树的算法来构造。例如banana的所有后缀:
0: banana 1: anana 2: nana 3: ana 4: na 5: a
按字典序排列后:
5: a 3: ana 1: anana 0: banana 4: na 2: nana
形成一个树形结构。
代码实现:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// banana中不重复的字符有:a b n
/*
* a b n
* n $ a a
* a n n $
* n $ a a
* a n $
* $ a
$*/
#define SIZE 27
#define Index(c) ((c) - ‘a‘)
#define rep(i, a, b) for(i = a; i < b; i++)
typedef struct BaseNode {
struct BaseNode*next[SIZE];
char c;
int num;
} suffix_tree, *strie;
void initialize(strie* root)
{
int i;
*root = (strie)malloc(sizeof(suffix_tree));
(*root)->c = 0;
rep(i, 0, SIZE) (*root)->next[i] = NULL;
}
void insert(strie*root, const char*str)
{
suffix_tree*node = *root, *tail;
int i, j;
for (i = 0; str[i] != ‘\0‘; i++)
{
if (node->next[Index(str[i])] == NULL)
{
tail = (strie)malloc(sizeof(suffix_tree));
tail->c = str[i];
rep(j, 0, SIZE) tail->next[j] = NULL;
node->next[Index(str[i])] = tail;
}
node = node->next[Index(str[i])];
}
rep(i, 0, SIZE) node->next[i] = NULL;
tail = (strie)malloc(sizeof(suffix_tree));
tail->c = ‘$‘;
rep(i, 0, SIZE) tail->next[i] = NULL;
node->next[SIZE - 1] = tail;
}
void show(suffix_tree*root)
{
if (root)
{
int i;
rep(i, 0, SIZE) show(root->next[i]);
printf("%c\n", root->c);
}
}
void destory(strie*root)
{
if (*root)
{
int i;
rep(i, 0, SIZE) destory(&(*root)->next[i]);
free(*root);
*root = NULL;
}
}
int main()
{
suffix_tree*root;
initialize(&root);
char str[] = "banana", *p = str;
while(*p)
{
insert(&root, p);
p++;
}
show(root);
destory(&root);
return 0;
}
上面算法中对于一串长m的字符串,建立一颗后缀字典树所需的时间为O(m2),27的循环在这里可看作常数,空间复杂度为O(m)。这里虽然也是O(m)的space,但倍数会比较大。
由于上面算法空间复杂度比较大,所以使用路径压缩以节省空间,这样的树就称为后缀树,也可以通过下标来存储,如图:
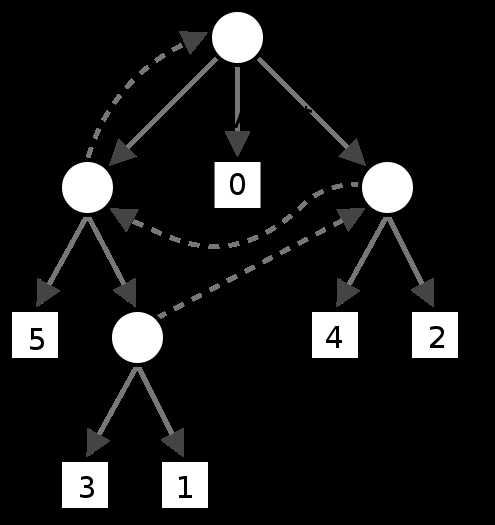
下面是代码是实现:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
/*
a banana na
na $ $ na $
na $ $
$
*/
#define SIZE 27
#define Index(c) ((c) - ‘a‘)
#define rep(i, a, b) for(i = a; i < b; i++)
typedef struct BaseNode {
struct BaseNode*next[SIZE];
char c;
char str[SIZE << 2];
int num;
} suffix_tree, *strie;
void initialize(strie* root)
{
*root = (strie)malloc(sizeof(suffix_tree));
(*root)->c = 0;
memset((*root)->str, 0, sizeof((*root)->str));
memset((*root)->next, 0, sizeof((*root)->next));
}
void insert(strie*root, const char*str)
{
suffix_tree*node = *root, *tail;
if (node->next[Index(str[0])] == NULL)
{
tail = (strie)malloc(sizeof(suffix_tree));
tail->c = 0;
strcpy(tail->str, str);
memset(tail->next, 0, sizeof(tail->next));
node->next[Index(str[0])] = tail;
}
node = node->next[Index(str[0])];
tail = (strie)malloc(sizeof(suffix_tree));
tail->c = ‘$‘;
memset(tail->str, 0, sizeof(tail->str));
memset(tail->next, 0, sizeof(tail->next));
node->next[SIZE - 1] = tail;
}
void show(suffix_tree*root)
{
if (root)
{
int i;
rep(i, 0, SIZE) show(root->next[i]);
printf("%s", root->str);
if(root->c)
printf("%c", root->c);
puts("");
}
}
void destory(strie*root)
{
if (*root)
{
int i;
rep(i, 0, SIZE) destory(&(*root)->next[i]);
free(*root);
*root = NULL;
}
}
int main()
{
suffix_tree*root;
initialize(&root);
char str[] = "banana", *p = str;
while(*p)
{
insert(&root, p);
p++;
}
show(root);
destory(&root);
return 0;
}
上面算法建立字符串的后缀树的时间复杂度为O(m),空间复杂度O(m)。
上面的都是对于一个字符串的处理方法,而广义后缀树将算法推广到了不同的字符串上,但我还没写过。
参考:https://en.wikipedia.org/wiki/Suffix_tree
原文:https://www.cnblogs.com/darkchii/p/9116558.html