1.学习总结

1.1图的思维导图

1.2 图结构学习体会

• 深度遍历算法：深度优先搜索，是图论中的经典算法。其利用深度优先搜索算法可以产生目标图的相应拓扑排序表，利用拓扑排序表可以方便的解决很多相关的图论问题，如最大路径问题等等。其的概念就是一条路走到黑。
• 广度遍历算法：广度优先是连通图的一种遍历策略。因为它的思想是从一个顶点V0开始，辐射状地优先遍历其周围较广的区域。其的概念就是左看看右看看，雨露均沾。
• Prim和Kruscal算法：p-在加权连通图里搜索最小生成树。即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小。由于和边数无关，和顶点树有关，所以适合求解稠密网的最小生成树。
•                                        k-求加权连通图的最小生成树的算法。对所有权值进行从小到大排序（这里对边排序时还需要记录边的索引，这样以边的权值排完序后只改变了权值的索引位置），然后每次选取最小的权值，如果和已有点集构成环则跳过，否则加到该点集中。最终有所有的点集构成的树就是最佳的。
  
• Dijkstra算法：典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。注意该算法要求图中不存在负权边。
• 拓扑排序算法：是将一个有向无环图G的所有的顶点排成一个线性序列，使得有向图中的任意的顶点u 和 v 构成的弧<u， v>属于该图的边集，并且使得 u 始终是出现在 v 的前面。

2.PTA实验作业

2.1 题目1：7-1 图着色问题

2.2 设计思路（伪代码或流程图）

将数组初始化为0；

令k=0；

寻找着色规范的点；

规范则输出；

否则重新着色；

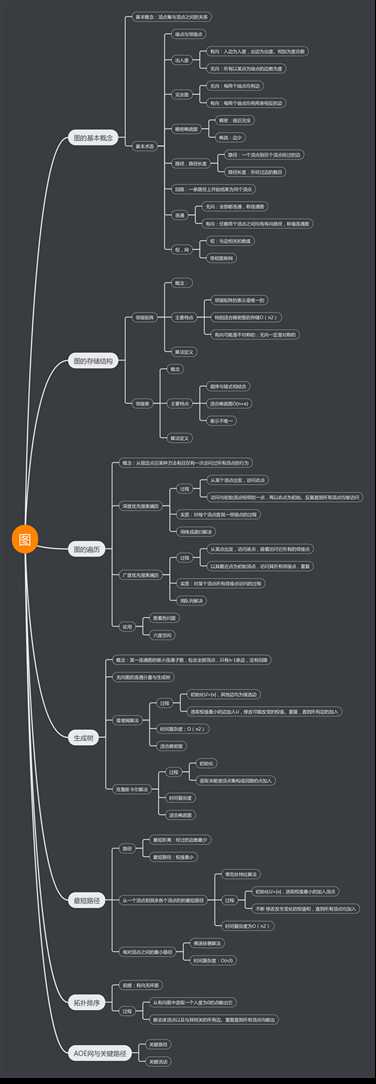
 2.3 代码截图

2.4 PTA提交列表说明

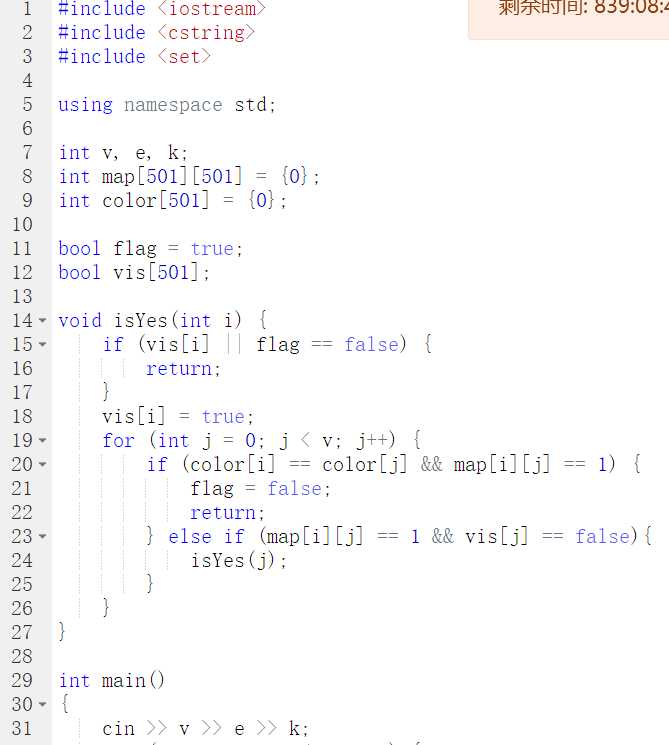
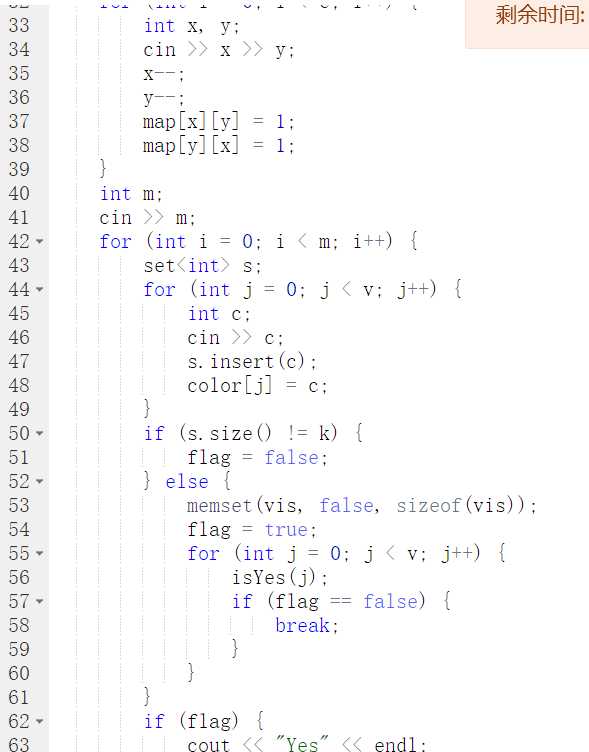
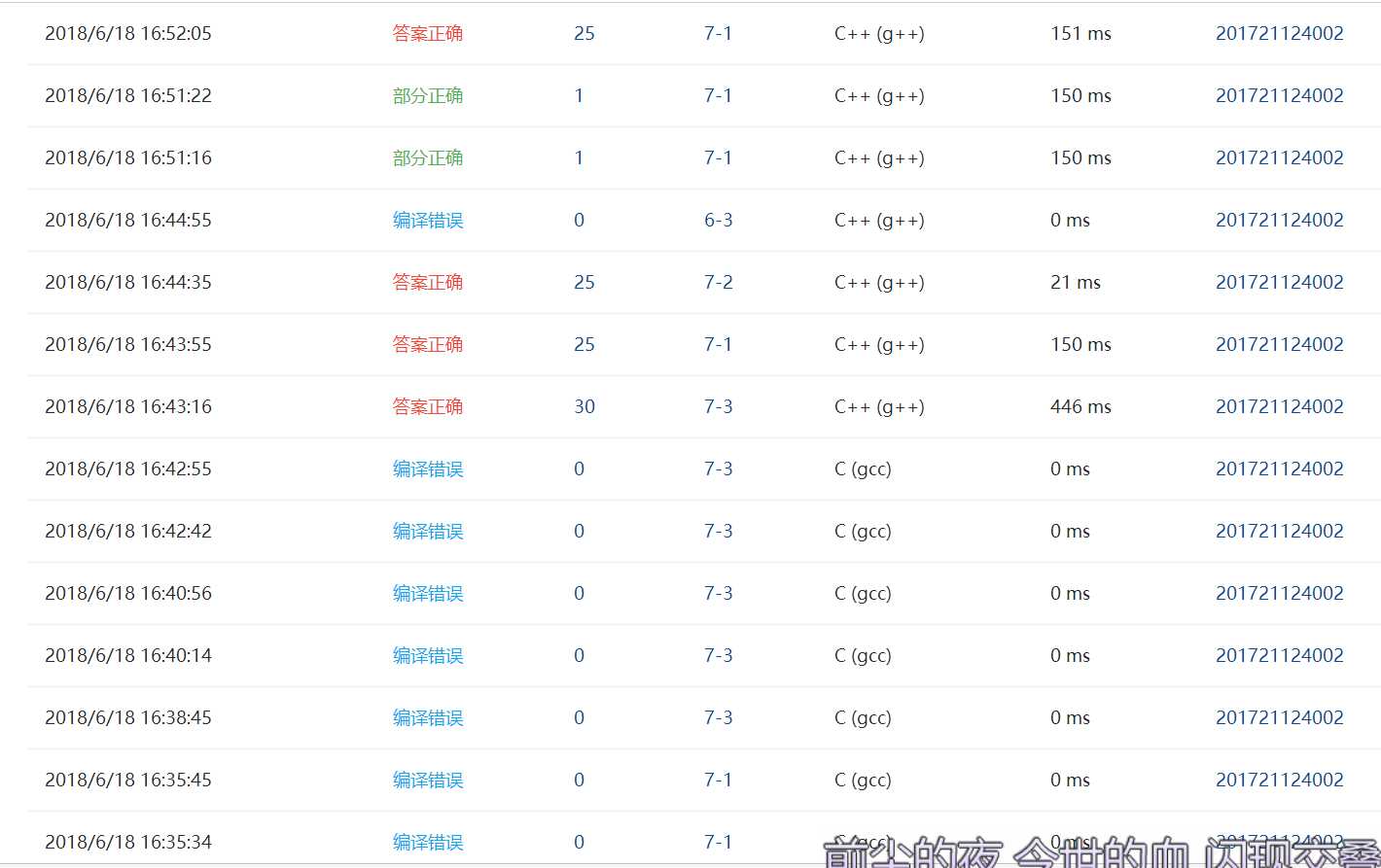
刚开始未注意到不同颜色的个数相加需等于k。

以及未把c改成c++。

2.2 题目2：7-2排座位

2.2 设计思路（伪代码或流程图）

初始化并查集；

判断两人是否为朋友；

是记录是朋友 ；否记录是敌人；

输入两个宾客；

有共同朋友就输出同一张桌子；

2.3 代码截图

2.4 PTA提交列表说明

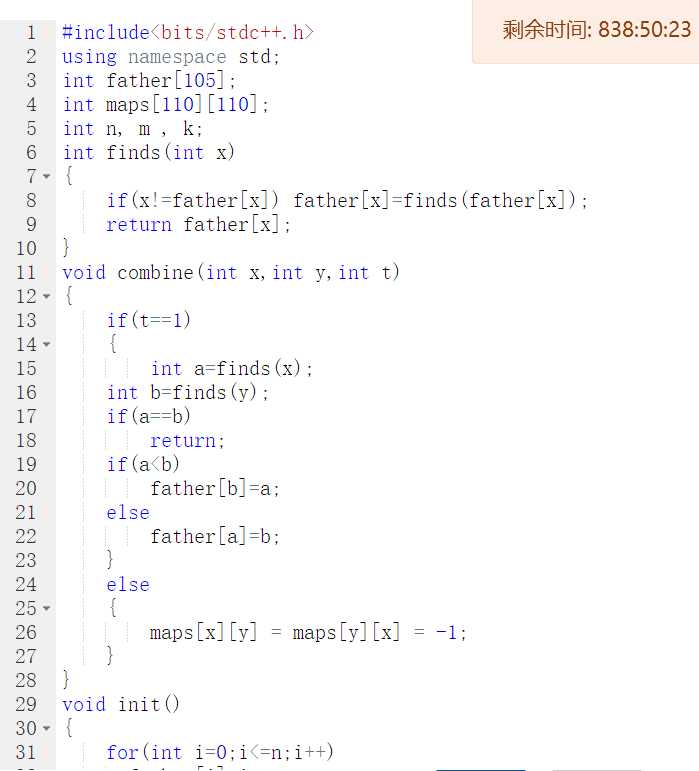
一开始不知如何判断两人是否为朋友关系，后用并查集解决，即只要判断是否处于同一棵树便能知两人是否处于同个朋友圈。

以及c未改成c++。

2.1 题目3：7-3 六度空间

2.2 设计思路（伪代码或流程图）

2.3 代码截图

2.4 PTA提交列表说明

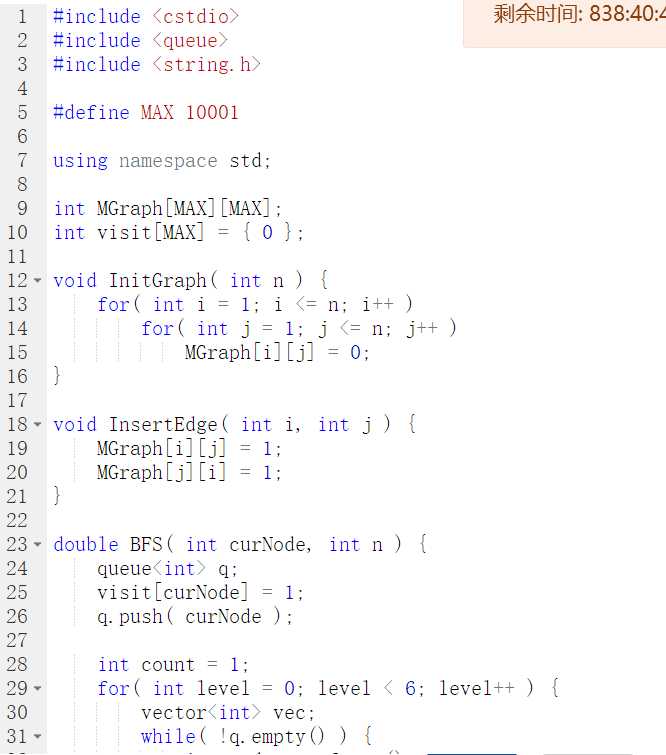
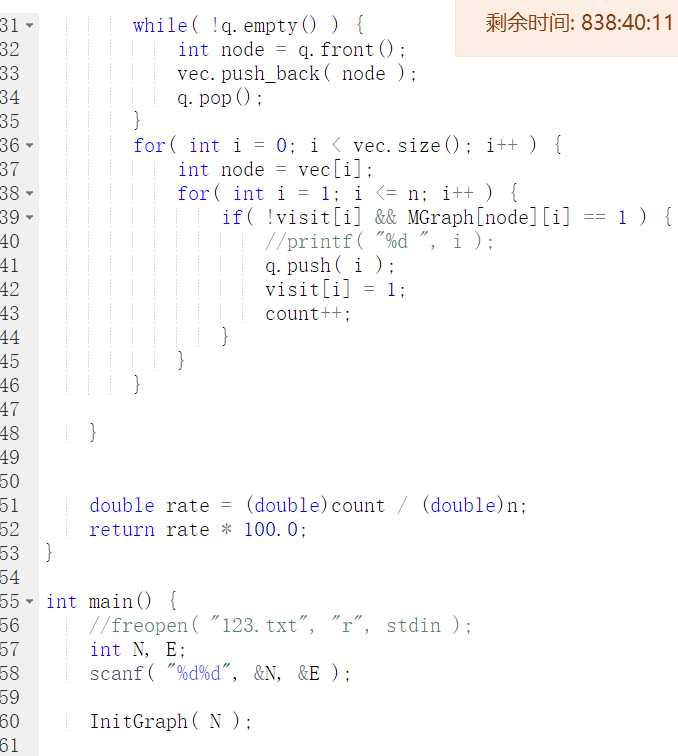
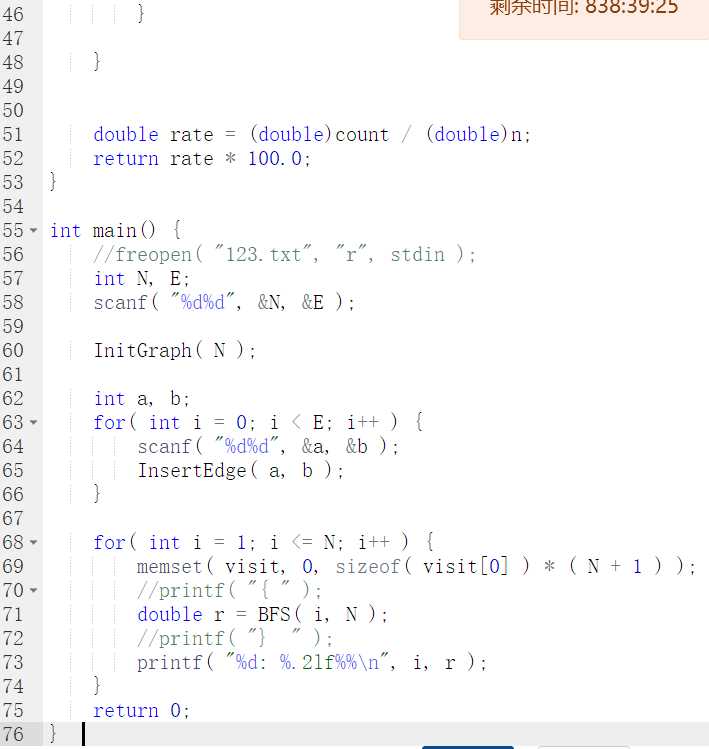
开始时未将函数初始化，导致错误。

以及c未换成c++。

3.截图本周题目集的PTA最后排名

4. 阅读代码

 void UFset() // 初始化 
 2 {
 3     for (int i = 0; i < n; i ++)
 4         parent[i] = -1;
 5 } 
 6 int Find(int x)  // 查找并返回结点x所属集合的根结点 
 7 {
 8     int s;    // 查找位置 
 9     for (s = x; parent[s]>=0; s = parent[s]);  // 注意这里的 ; 
10     while (s != x)   // 优化方案 -- 压缩路径，使后续的查找 
11     {
12         int tmp = parent[x];
13         parent[x] = s;
14         x = tmp;
15     }
16     return s;
17 }
18 // R1和R2是两个元素，属于两个不同的集合，现在合并这两个集合
19 void Union (int R1, int R2)
20 {
21     // r1位R1的根结点，r2位R2的根结点
22     int r1 = Find(R1), r2 = Find(R2);
23     int tmp = parent[r1] + parent[r2];   // 两个集合的结点个数之和（负数） 
24     // 如果R2所在树结点个数 > R1所在树结点个数
25     // 注意parent[r1]和parent[r2]都是负数
26     if(parent[r1] > parent[r2])    // 优化方案 -- 加权法则 
27     {
28         parent[r1] = r2;        // 将根结点r1所在的树作为r2的子树（合并） 
29         parent[r2] = tmp;       // 跟新根结点r2的parent[]值 
30     }
31     else
32     {
33         parent[r2] = r1;         // 将根结点r2所在的树作为r1的子树（合并） 
34         parent[r1] = tmp;        // 跟新根结点r1的parent[]值 
35     } 

图作业

原文：https://www.cnblogs.com/hxfa/p/9195855.html