1.学习总结

1.1图的思维导图

1.2 图结构学习体会

• 深度优先遍历与广度优先遍历算法应该说是图中最基本的两个算法，许多算法都带有深度遍历与广度遍历的影子，所以是必须掌握的。
• 克鲁斯卡尔算法是比普里姆算法更为精确的算法，但对于规模较大的最小生成树问题，求解速度较慢，所以稀疏图用克鲁斯卡尔算法，而稠密图用普里姆算法求解。
• 在最小生成树中从一个顶点到另一顶点的路径不一定是最短的，但在狄克斯特拉树中从根结点到每个叶子结点的路径都是最短的。
• 只有有向无环图才可以进行拓扑排序，所以拓扑排序可以用来判断图中是否存在环。

2.PTA实验作业

2.1.1 题目1：图着色问题

2.1.2 设计思路

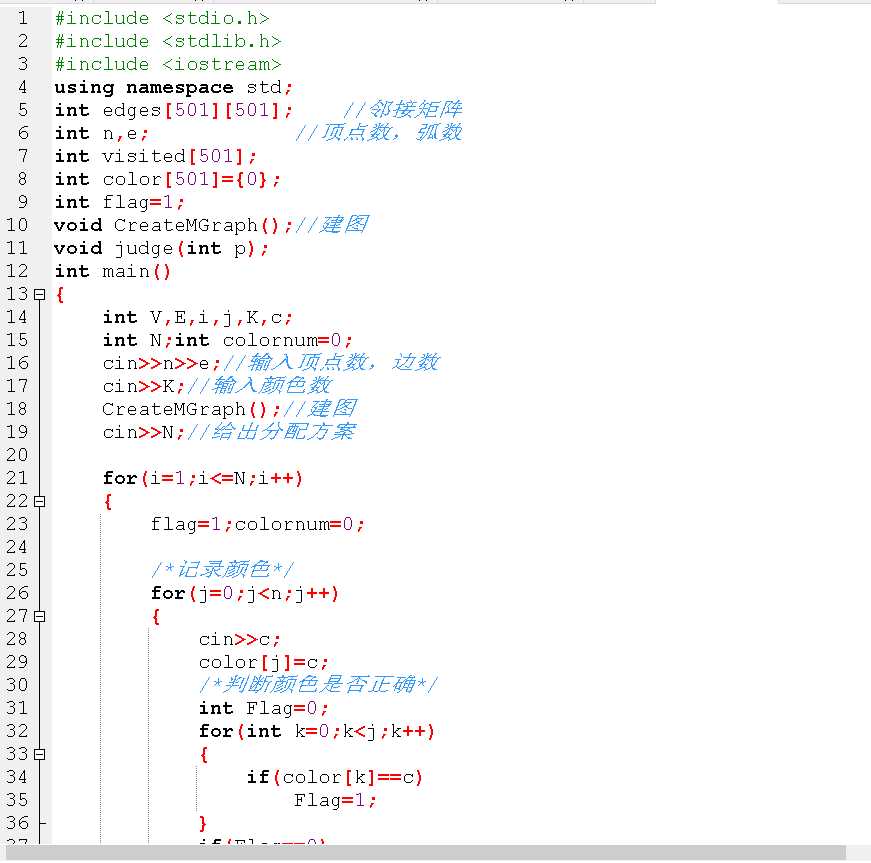
int main()
{
    CreateMGraph();//建图
   
    for i=0 to N
        flag=1;colornum=0;//颜色数量
        for j=0 to n
            输入颜色;颜色数组存储颜色
            int Flag=0;
            for k=0 to k<j
                if 颜色数组中存在与当前颜色相同的，则判断错误，即Flag=1
            if 颜色正确
                颜色数量加一
        if 颜色数量不为K，判断为错误，即flag=0
        if 颜色数量正确
            for j=0 to n
                for k=0 to n 
                    judge(j);//进入函数判断配色方案是否正确
                    if flag==0
                        break;//停止循环
        if flag==1 输出 Yes
        else 输出 No
}
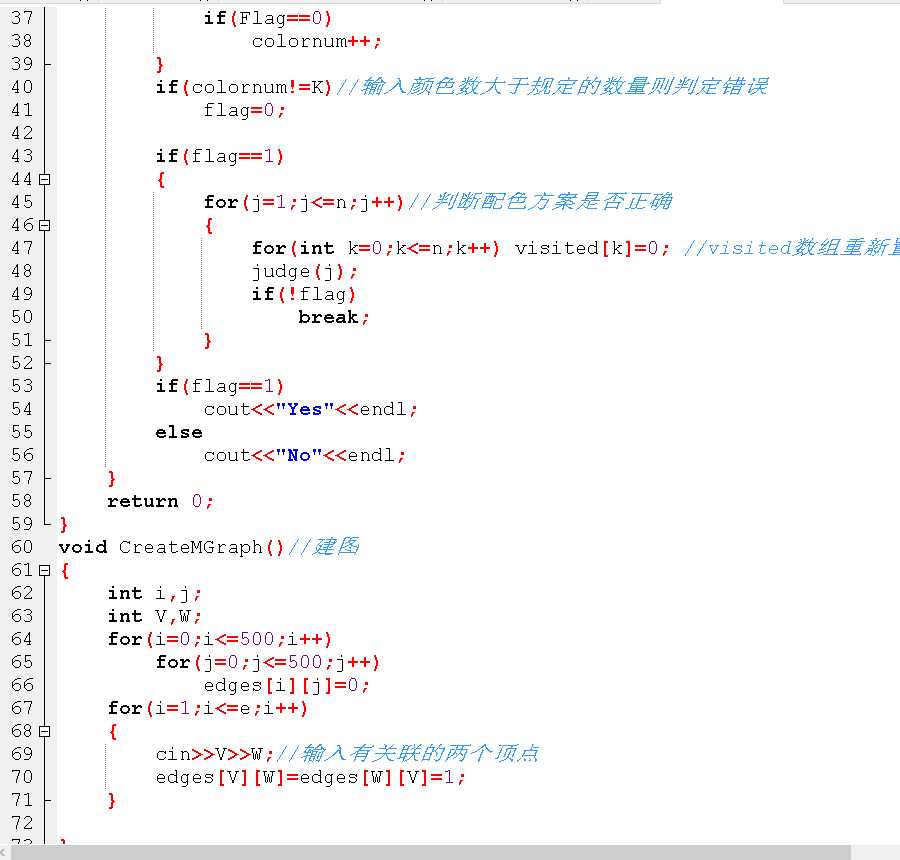
void judge(int p)
{
    if p遍历过 或 此时flag为0,则不再进行任何操作
    else
        标记p遍历过
        for i=0 to n
            if p与i有关联，即edges[p][i]==1
                if p处颜色与i处颜色相同
                    flag=0 并且停止循环
                else if i未遍历过
                    i进入函数judge进行递归
}

2.1.3 代码截图

2.1.4 PTA提交列表说明

• 1.结构体中无法定义过大的数组
• 2.缺少判断颜色数量是否正确的操作
• 3.忘记将visited数组重置为0
• 4.还有错误存在，但目前未找出来

2.2.1 题目2：公路村村通

2.2.2 设计思路

/*由普里姆算法改造*/
int prime(int n)
{
        cost[1]=0;   //初始化
        for i=2 to n   
            cost[i]=road[1][i];
        for i=1 to n
            min初始为一个极大值
            for j=1 to n
                if 通往j的费用不为0 且 小于 min
                    min=cost[j];k=j;
            if k!= 0
                num=cost[k]+num;//记录最小费用
                cost[k]=0;   // 作为记录过的标志
                for j=1 to n
                    if j未访问过 且 k到j的费用小于当前j的费用
                        cost[j]=coad[k][j];
                else
                    输出 -1;flag=1;退出结束循环
        if flag==0
            输出最低成本
}

2.2.3 代码截图

2.2.4 PTA提交列表说明

第一次提交时只有第一个测试点对，调试的时候发现当k==0时即表示找不到最小路径，此时就可以停止循环退出，多考虑反而会导致结果错误，但是仍有一个测试点不对，最后的通过是在完成7-7 即旅游规划那道题后面，尝试着也在数组初始化的时候做修改，于是通过了。

2.3.1 题目3：旅游规划

2.3.2 设计思路

/*该道题主要运用狄克斯特拉算法*/
void Dijkstra(int n,int c1,int c2)
{
    for i=0 to n   //初始化
        cost[i]=fare[c1][i];
        dist[i]=city[c1][i];
    visited[c1]=1;dist[c1]=0;
    for i=0 to n      //找出距离c1最小的点
        mindis初始化为最大数值
        for j=0 to n
            if j点未访问过 且 j到c1的距离小于mindis
                k=j;
                mindis=dist[j];//更新最小距离
        for j=0 to n      //修改未访问过顶点的距离
            if j未访问过
                    if k到j的距离加上此时最小距离小于j到c1的距离，改变j的数值
                        dist[j]=dist[k]+city[k][j];
                        cost[j]=cost[k]+fare[k][j];
                    else if 距离相同 且 所用费用小于此时总费用
                        cost[j]=cost[k]+fare[k][j];
}

2.3.3 代码截图

2.3.4 PTA提交列表说明

之前提交的时候只有第一个测试点是对的，上课的时候听同学讲矩阵中对角线初始为0，其余设为最大值，考虑到本题要求不大于500，INF就设为501，但是提交后发现当N,M为最大值时段错误，将初始数组的范围由M改成501，就对了。

3.截图本周题目集的PTA最后排名

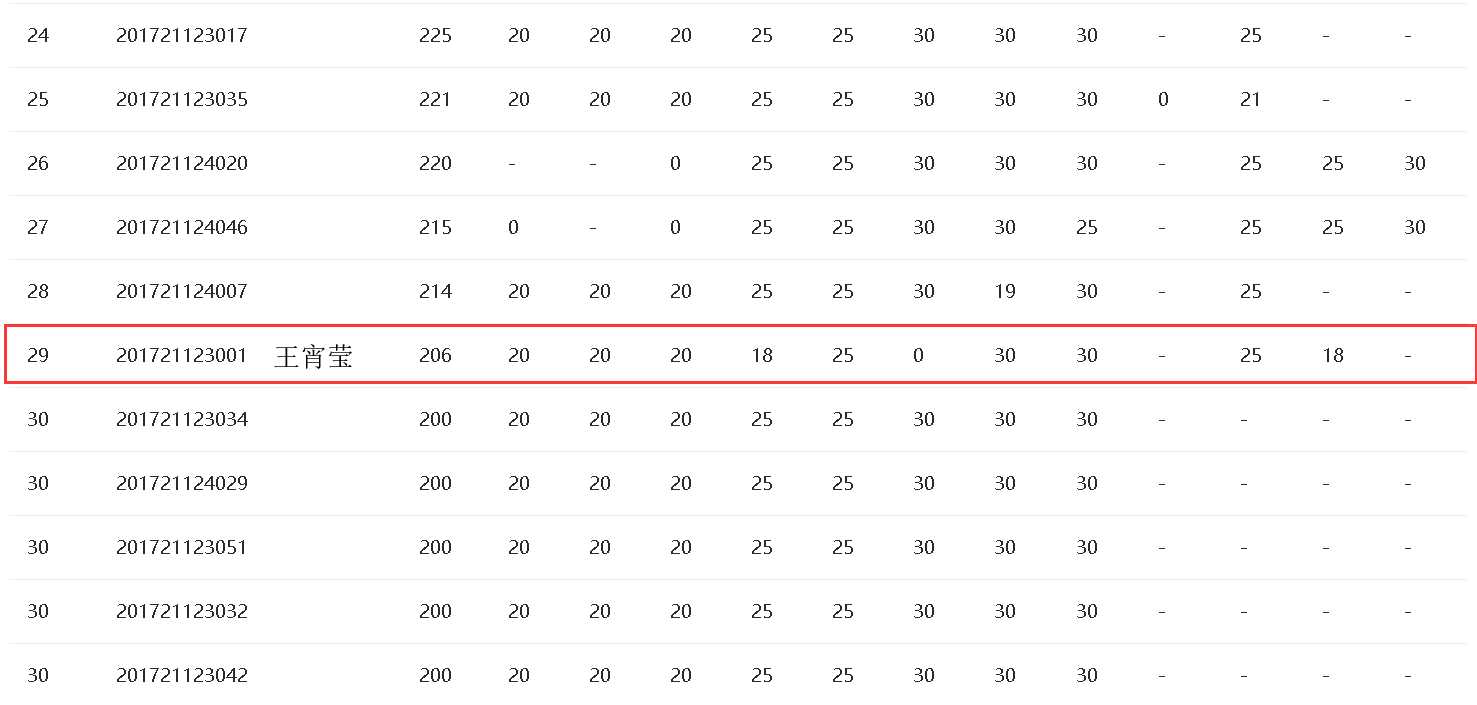
本次题目集总分：310分

3.1 PTA排名

3.2 我的总分：206

4. 阅读代码

利用图完成数独

#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define ULL unsigned long long
typedef pair<int,int>pii;

const int N = 20;
const int mod = 765431;

int n=9;
char mp[N][N];  //  原图
char opt[N][N]; // 中间图
bool vol[N][N],row[N][N]; //row[i][j] 第i行中已经有j数字，vol[i][j]第i列中已经有j数字
pii P[100];int sz; // 存储所有的未知位置
int flag;

bool check(int now,int val){  // 查询 3*3宫
    pii p = P[now];
    int n=(p.first-1)/3*3;
    int m=(p.second-1)/3*3;

    for(int i=n+1;i<=n+3;i++){
        for(int j=m+1;j<=m+3;j++){
            if(opt[i][j] == val+‘0‘) return false;
        }
    }
    return true;
}

void dfs(int now){
    if(flag) return ;
    if(now==sz) {
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++) {
                if(j!=1) putchar(‘ ‘);
                printf("%c",opt[i][j]);
            }
            puts("") ;
        }
        flag=1;
        return ;
    }

    pii p = P[now];
    for(int j=1;j<=9;j++){
        if( !row[p.first][j] && !vol[p.second][j] && check(now,j)){
            row[p.first][j]=1; vol[p.second][j]=1;
            opt[p.first][p.second]=j+‘0‘;
            dfs(now+1);
            row[p.first][j]=0; vol[p.second][j]=0;
            opt[p.first][p.second]=mp[p.first][p.second];
        }
    }
}

int main(){
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            scanf("%c",&mp[i][j]);
            opt[i][j]=mp[i][j];
            if(mp[i][j] == ‘*‘) {
                P[sz].first=i;
                P[sz++].second=j;
            }else {
                int val=mp[i][j]-‘0‘;
                vol[j][val]=1;
                row[i][val]=1;
            }
        }
        getchar();
    }
    flag=0;
    dfs(0);
    return 0 ;
}

前不久在玩数独，碰巧看到了用图来解决数独问题，觉得很有意思。

数独游戏要求九宫格中每一行每一列不能有重复的数字出现，那么就意味着这个程序需要不断进行比较判断,不能出现重复的数字。首先利用深度遍历往宫格里填数字，然后检查在该数字所处的行列是否有出现过，再在3*3的宫格里判断是否有相同的数字，若最后结果都不行则需要改变宫格中的数字，再次判断。

测试结果：

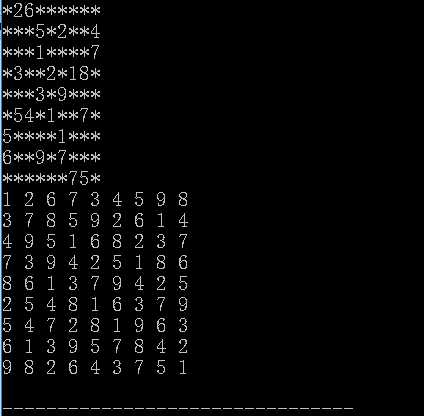
博客指路→(https://blog.csdn.net/qq_37383726/article/details/79703157)

博客作业06--图

原文：https://www.cnblogs.com/wwwwxy128/p/9185079.html