Kiana 最近沉迷于一款神奇的游戏无法自拔。
简单来说,这款游戏是在一个平面上进行的。
有一架弹弓位于 (0,0) 处,每次 Kiana 可以用它向第一象限发射一只红色的小鸟,小鸟们的飞行轨迹均为形如 y=ax^2+bx的曲线,其中 a,b是Kiana 指定的参数,且必须满足 a<0,a,b 都是实数。
当小鸟落回地面(即 x 轴)时,它就会瞬间消失。
在游戏的某个关卡里,平面的第一象限中有 n 只绿色的小猪,其中第 i 只小猪所在的坐标为 (xi?,yi?) 。
如果某只小鸟的飞行轨迹经过了 (xi?,yi?) ,那么第 i 只小猪就会被消灭掉,同时小鸟将会沿着原先的轨迹继续飞行;
如果一只小鸟的飞行轨迹没有经过 (xi?,yi?) ,那么这只小鸟飞行的全过程就不会对第 i 只小猪产生任何影响。
例如,若两只小猪分别位于 (1,3) 和 (3,3) ,Kiana 可以选择发射一只飞行轨迹为 y=-x^2+4x 的小鸟,这样两只小猪就会被这只小鸟一起消灭。
而这个游戏的目的,就是通过发射小鸟消灭所有的小猪。
这款神奇游戏的每个关卡对 Kiana来说都很难,所以Kiana还输入了一些神秘的指令,使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。
假设这款游戏一共有 T 个关卡,现在 Kiana想知道,对于每一个关卡,至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算,所以希望由你告诉她。
输入格式:
第一行包含一个正整数 T ,表示游戏的关卡总数。
下面依次输入这 T 个关卡的信息。每个关卡第一行包含两个非负整数 n,mn,m ,分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。接下来的 n 行中,第 ii 行包含两个正实数 xi?,yi? ,表示第 i 只小猪坐标为 (xi?,yi?)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。
如果 m=0 ,表示Kiana输入了一个没有任何作用的指令。
如果 m=1 ,则这个关卡将会满足:至多用 ?n/3+1? 只小鸟即可消灭所有小猪。
如果 m=2 ,则这个关卡将会满足:一定存在一种最优解,其中有一只小鸟消灭了至少 ?n/3? 只小猪。
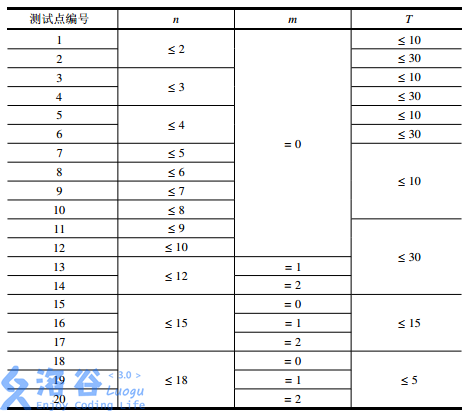
保证 1≤n≤18 , 0≤m≤2 , 0<xi?,yi?<10 ,输入中的实数均保留到小数点后两位。
上文中,符号 ?c? 和 ?c? 分别表示对 c 向上取整和向下取整,例如: ?2.1?=?2.9?=?3.0?=?3.0?=?3.1?=?3.9?=3 。
输出格式:
对每个关卡依次输出一行答案。
输出的每一行包含一个正整数,表示相应的关卡中,消灭所有小猪最少需要的小鸟数量。
输入样例#1:
2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00
输出样例#1:
1
1
输入样例#2:
3
2 0
1.41 2.00
1.73 3.00
3 0
1.11 1.41
2.34 1.79
2.98 1.49
5 0
2.72 2.72
2.72 3.14
3.14 2.72
3.14 3.14
5.00 5.00
输出样例#2:
2
2
3
输入样例#3:
1
10 0
7.16 6.28
2.02 0.38
8.33 7.78
7.68 2.09
7.46 7.86
5.77 7.44
8.24 6.72
4.42 5.11
5.42 7.79
8.15 4.99
输出样例#3:
6
【样例解释1】
这组数据中一共有两个关卡。
第一个关卡与【问题描述】中的情形相同,2只小猪分别位于 (1.00,3.00) 和 (3.00,3.00) ,只需发射一只飞行轨迹为 y = -x^2 + 4x 的小鸟即可消灭它们。
第二个关卡中有 5 只小猪,但经过观察我们可以发现它们的坐标都在抛物线 y = -x^2 + 6x 上,故Kiana只需要发射一只小鸟即可消灭所有小猪。
【数据范围】
这道题有三种做法:强力剪枝搜索,记忆化搜索,状压dp,这里主要讲状压dp的做法
题目要求我们用最少的小鸟击落所有的猪,而小鸟的运动轨迹是一条抛物线,那么我们就想可不可以枚举两个不同的小鸟来来确定这条抛物线呢?这是肯定的,因为这条抛物线只有两个参数a,b,我们将两个小鸟的坐标带入进去就可以求得这两个参数,解二元一次方程,这应该是初中数学内容
\(a*x_1^2+b*x_1=y_1\)
\(a*x_2^2+b*x_2=y_2\)
得到
\(a=(x_2*y_1-x_1*y_2)/(x_1^2*x_2-x_2^2*x_1);\)
\(b=(x_1^2*y_2-x_2^2*y_1)/(x_1^2*x_2-x_2^2*x_1);\)
然后要注意\(x_1^2*x_2-x_2^2*x_1!=0\),即分母不能为0求出这条抛物线后,我们就可以预处理这条抛物线打下了哪些猪,可以用一个二位数组f[i][j]保存通过枚举i和j这两个猪所构成的抛物线打下了哪些猪
bool check(double a,double b){
return fabs(a-b)<=1e-6;
}
bool c(double x1,double y1,double x2,double y2){
if(x2*x2*x1!=x1*x1*x2){
a=(y2*x1-x2*y1)/(x2*x2*x1-x1*x1*x2);
b=(x1*x1*y2-x2*x2*y1)/(x1*x1*x2-x2*x2*x1);
}
if(a<0) return 1;
return 0;
}
void init(){
for(int i=1;i<n;i++){
for(int j=i+1;j<=n;j++){
if(check(x[i],x[j])) continue;
if(c(x[i],y[i],x[j],y[j])){
for(int k=1;k<=n;k++){
if(fabs(a*x[k]*x[k]+b*x[k]-y[k])<=1e-6) f[i][j]|=1<<(k-1);
}
}
}
}
}注意:题目要求a<0,所以碰到a>0的情况就要舍去,fabs是取浮点数的绝对值,虽然abs也可用但是慢很多
然后就是标准的状压dp,状态转移方程为dp[sta|f[i][j]]=min(dp[sta|f[i][j]],dp[sta]+1),这里的f[i][j]指的是是合法的抛物线
#include<bits/stdc++.h>
#define MIN(a,b) (a)>(b)?(b):(a)
#define MAX(a,b) (a)>(b)?(a):(b)
#define in(i) (i=read())
using namespace std;
map<int,int>mp;
int read(){
int ans=0,f=1;
char i=getchar();
while(i<'0'||i>'9'){
if(i=='-') f=-1;
i=getchar();
}
while(i>='0' && i<='9'){
ans=(ans<<1)+(ans<<3)+i-'0';
i=getchar();
}
return ans*f;
}
double x[19],y[19];
int n,m,T;
int dp[1<<18];
int f[19][19];
double a,b;
bool check(double a,double b){
return fabs(a-b)<=1e-6;
}
bool c(double x1,double y1,double x2,double y2){
if(x2*x2*x1!=x1*x1*x2){
a=(y2*x1-x2*y1)/(x2*x2*x1-x1*x1*x2);
b=(x1*x1*y2-x2*x2*y1)/(x1*x1*x2-x2*x2*x1);
}
if(a<0) return 1;
return 0;
}
void init(){
for(int i=1;i<n;i++){
for(int j=i+1;j<=n;j++){
if(check(x[i],x[j])) continue;
if(c(x[i],y[i],x[j],y[j])){
for(int k=1;k<=n;k++){
if(fabs(a*x[k]*x[k]+b*x[k]-y[k])<=1e-6) f[i][j]|=1<<(k-1);
}
}
}
}
}
void DP(){
dp[0]=0;
int tot=1<<n;
for(int i=0;i<tot;i++){
for(int j=1;j<=n;j++){
if(!(i&(1<<(j-1)))){
dp[i|(1<<(j-1))]=MIN(dp[i|(1<<(j-1))],dp[i]+1);
for(int k=j+1;k<=n;k++){
if(!check(x[j],x[k])){
dp[i|f[j][k]]=MIN(dp[i|f[j][k]],dp[i]+1);
}
}
}
}
}
}
int main()
{
in(T);
for(int t=1;t<=T;t++){
memset(dp,127,sizeof(dp));
memset(f,0,sizeof(f));
in(n);in(m);
for(int i=1;i<=n;i++) scanf("%lf%lf",&x[i],&y[i]);
init();DP();
printf("%d\n",dp[(1<<n)-1]);
}
return 0;
}原文:https://www.cnblogs.com/real-l/p/9157479.html