Stirling数反演相关内容:http://blog.csdn.net/OwenOwl/article/details/79442341
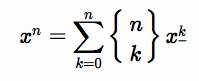
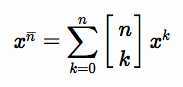
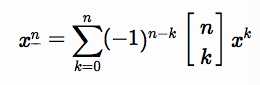
下降幂是指$x*(x-1)*(x-2)*...*(x-k+1)$,上升幂是指$x*(x+1)*(x+2)*...*(x+k-1)$
接着我们考虑斯特林数反演
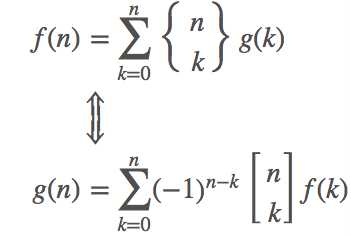
可以发现将通常幂和下降幂分别作为f(x)和g(x),就可以直接反演了。
然后有一个概念叫作离散微积分(有限微积分),就是将积分的概念在整数范围内实现。
https://ruanx.pw/post/有限微积分.html
现在就可以做自然数幂和了:https://www.cnblogs.com/meowww/p/6410869.html 方法二
注意这里有个笔误
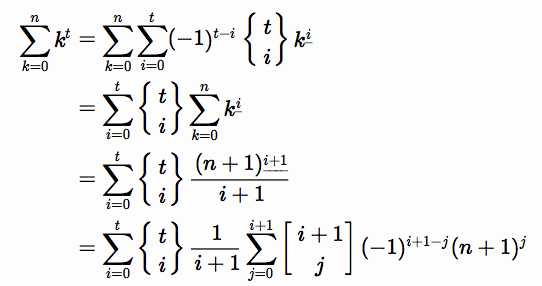
第一个等式后面没有$(-1)^{t-i}$
这样我们就可以在$O(k^2)$内求出答案了,这是相当优秀的复杂度。
