一、卡特兰数(Catalan number)
1.定义
组合数学中一个常出现在各种计数问题中出现的数列(用c表示)。以比利时的数学家欧仁·查理·卡特兰的名字来命名;
2.计算公式
(1)递推公式
c[n]=Σc[k]*c[n-k-1],边界条件为c[0]=1;
其递推解为c[n]=C(2n,n)/(n+1),即卡特兰数的通项公式,其中C表示数的组合;
(2)另类递推式
c[n]=c[n-1](4n-2)/(n+1),边界条件为c[0]=1;
其递推解为c[n]=C(2n,n)-C(2n,n-1),C表示数的组合;
(3)其他公式
c[n]=(Σ(0≤i≤n)C(i,n)^2)/(n+1);
ps:通过展开可以发现它们的本质是一样的;
3.简单应用
(1)求解路径方案数:如图所示,从原点(0,0)到点B(n,n),只能向右或向上进行长度为一个单位的移动,路线一直处于y=x之下(不越过直线y=x)的不同路径方案数;
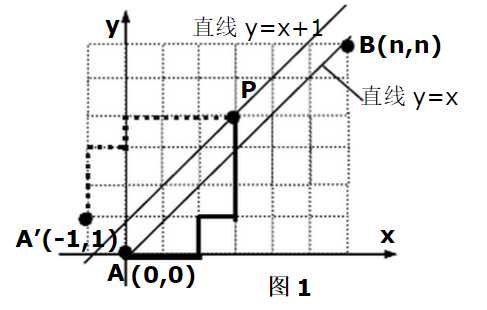
solution:每个n的解都可以看做先前的解数(再向右向上即为所求)加上不触及各个y=x上的点到达B点的方案数,可以发现其递推公式即为卡特兰数计算公式;
(2)求01串的个数:n个0与n个1构成的序列方案数,使得任何一个前缀0的个数不少于1的个数;
solution:将0看做在坐标系中向右走一步,1看做向上走一步,则问题即可化简为从原点到(n,n)所有路线中一直处于y=x之下(不越过直线y=x)的不同路径方案数,与上题相同,方案数即为对应n的卡特兰数;
(3)给定节点求解二叉树的个数:已知由n个节点,求形成不同的二叉树有多少种?
solution:将向左生成子树看做0,向右生成字数看成1,则问题化简为求n/2个0和n/2个1构成数串的不同方案数,即上题无条件解的一半,与上题答案相同,形成不同的树的个数即为对应n的卡特兰数;
(4)求凸边形进行三角剖分的不同方案数:在一个有n+1条边的凸多边形中,求通过若干条互不相交的对角线,把这个多边形划分成若干个三角形的不同方案数。
solution:因为每一条边都一定是剖分后的三角形的一条边,任意一条边都会把多边形分成两个小多边形,那么根据乘法原理,解即为划分成不同多边形的方案数对应小多边形的划分方案数之和,即f[n]=Σ(3≤k≤n-3)f[k]f[n-k-1],可以发现解数即为n对应的卡特兰数;
浅谈卡特兰数(Catalan number)的原理和应用
原文:https://www.cnblogs.com/COLIN-LIGHTNING/p/8450053.html
