一.数学模型
1.算法的时间复杂度和 执行每条语句的频率 有关
2.常见的增长数量级函数
| 描述 函数 |
| 常数级别 1 |
| 对数级别 logN |
| 线性级别 N |
| 线性对数级别 NlogN |
| 平方级别 N^2 |
| 立方级别 N^3 |
| 指数级别 2^N |
3.增长数量级的分类

4.归并排序是线性对数级别的(NlogN),二分查找是对数级别的(logN)
在N个排序的数中二分查找的频率为logN,即每次查找的时间复杂度都为logN
5.典型的增长数量级函数
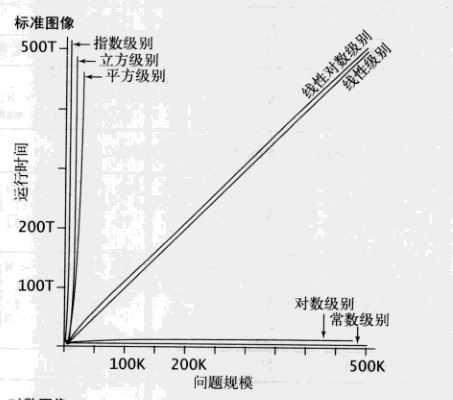
一.数学模型
1.算法的时间复杂度和 执行每条语句的频率 有关
2.常见的增长数量级函数
| 描述 函数 |
| 常数级别 1 |
| 对数级别 logN |
| 线性级别 N |
| 线性对数级别 NlogN |
| 平方级别 N^2 |
| 立方级别 N^3 |
| 指数级别 2^N |
3.增长数量级的分类

4.归并排序是线性对数级别的(NlogN),二分查找是对数级别的(logN)
在N个排序的数中二分查找的频率为logN,即每次查找的时间复杂度都为logN
5.典型的增长数量级函数

原文:https://www.cnblogs.com/midiyu/p/8412853.html