BZOJ3231
http://www.lydsy.com/JudgeOnline/problem.php?id=3231
luogu2461
https://www.luogu.org/problemnew/show/2461
这题代码在本地过编译,但在BZOJ过不了编译,只好在luogu上交
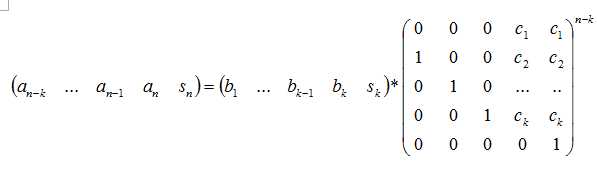
大致就是构造这样一个矩阵,然后快速幂
复杂度O(k3log n)
#include<cstdio>
#define ROF(i,s,t) for(register int i=s;i>=t;--i)
#define FOR(i,s,t) for(register int i=s;i<=t;++i)
typedef long long ll;
int k;
ll n,m;
int p,ansn,ansm;
struct matrix{
static int a[17][17];
inline matrix(){FOR(i,0,k)FOR(j,0,k)a[i][j]=0;}
inline int *operator[](int x){return a[x];}
inline matrix operator*(matrix A)const{
matrix ret;
FOR(i,0,k)
FOR(j,0,k)
FOR(l,0,k){
ret[i][j]+=(int)(1ll*a[i][l]*A[l][j]%p);
ret[i][j]%=p;
}
return ret;
}
}A,B,C,D;
inline void fp(ll b){
while(b){
if(b&1)C=C*D;
D=D*D;
b>>=1;
}
}
inline int getans(ll x){
C=A;D=B;
ll ret=0;
if(x<=k){
FOR(i,0,x-1)
ret+=A[0][i],ret%=p;
return ret;
}
fp(x-k);
return C[0][k];
}
int main(){
scanf("%d",&k);
FOR(i,0,k-1)scanf("%d",&A.a[0][i]);
ROF(i,k-1,0)scanf("%d",&B.a[i][k-1]);
scanf("%lld%lld%d",&m,&n,&p);
FOR(i,0,k-1)A[0][i]%=p,A[0][k]+=A[0][i],A[0][k]%=p;
FOR(i,0,k-1)B[i][k-1]%=p,B[i][k]=B[i][k-1];
B[k][k]=1;
FOR(i,0,k-2)B[i+1][i]=1;
ansm=getans(m-1ll);
ansn=getans(n);
printf("%d\n",(ansn-ansm+p)%p);
return 0;
}
BZOJ2875
http://www.lydsy.com/JudgeOnline/problem.php?id=2875
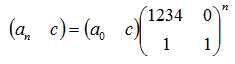
都是套路题用矩乘优化线性递推式
#include<cstdio>
#include<iostream>
#define FOR(i,s,t) for(register int i=s;i<=t;++i)
using namespace std;
typedef long long ll;
ll n,m,x,g,a,c;
inline ll mul(ll a,ll b){
ll res=0;
while(b){
if(b&1)res=(res+a)%m;
a=(a<<1)%m;
b>>=1;
}
return res;
}
struct matrix{
ll a[3][3];
inline void clean(){
FOR(i,1,2)
FOR(j,1,2)
a[i][j]=0;
}
inline matrix operator*(matrix A)const{
matrix B;
B.clean();
FOR(i,1,2)
FOR(j,1,2)
FOR(k,1,2){
B.a[i][j]+=1ll*mul(a[i][k],A.a[k][j])%m;
B.a[i][j]%=m;
}
return B;
}
}A,B;
inline matrix fp(matrix B,ll b){
matrix ret;
ret.clean();
ret.a[1][1]=1;
ret.a[2][2]=1;
while(b){
if(b&1)ret=ret*B;
B=B*B;
b>>=1;
}
return ret;
}
int main(){
cin>>m>>a>>c>>x>>n>>g;
B.a[1][1]=a;
B.a[2][1]=c;
B.a[2][2]=1;
B=fp(B,n);
A.a[1][1]=x;
A.a[1][2]=1;
A=A*B;
cout<<A.a[1][1]%g<<‘\n‘;
return 0;
}
