纪念莫比乌斯反演首题!同时感谢Antileaf学长的耐心讲解!
我们可以用容斥原理搞
令f(d)为1<=x<=n,1<=y<=m且gcd(x,y)=d的数对(x,y)的个数
则可设:
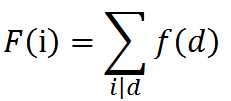
可得F(i)为1<=x<=n,1<=y<=m且i|gcd(x,y)的数对(x,y)的个数
化简可得

莫比乌斯反演一下

枚举i的每一个倍数d,我们就可以O(n)询问了
但是这样明显不行,所以我们还需要优化:
设![]() ,可以得到
,可以得到
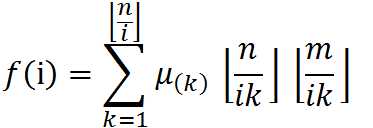
我们设![]() ,
,![]() ,则可以得到
,则可以得到
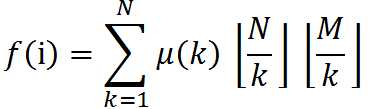
我们注意到,枚举k的时候,对于一些k,后边向下取整的值是相等的
那么在相等的区间内的答案,就是这一段区间的μ值之和*后边的不变的部分
μ值之和可以用前缀和搞出来,可是怎么找这一段呢
借鉴PoPoQQQ的打法:
if(n>m) swap(n,m);
for(i=1;i<=n;i=last+1)
{
last=min(n/(n/i),m/(m/i));
res+=(n/i)*(m/i)*(sum[last]-sum[i-1]);//sum是μ的前缀和
}
return res;
可以感性理解为对于两个n,m,向下取整相等的分别可以划分成一段一段的。
因为我们要的一段区间是n与m对于k向下取整都不变 ,所以我们去它们的一段段的公共区间就可以了
这是一道比较典型的例题,贴上代码:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define pos(i,a,b) for(int i=(a);i<=(b);i++)
#define N 50100
int mu[N],prime[N],notprime[N],sum[N];
void getmu(){
mu[1]=1;
pos(i,2,N-10){
if(!notprime[i]){
prime[++prime[0]]=i;
mu[i]=-1;
}
for(int j=1;j<=prime[0]&&prime[j]*i<=N-10;j++){
notprime[prime[j]*i]=1;
if(i%prime[j]==0){
mu[prime[j]*i]=0;break;
}
mu[prime[j]*i]=-mu[i];
}
}
sum[0]=mu[0];
pos(i,1,N-10) sum[i]=sum[i-1]+mu[i];
}
int a,b,c,d,k,n,m;
int getans(int x,int y){
if(x>y) swap(x,y);
n=x/k;m=y/k;
int last(0),ans(0);
for(int i=1;i<=n;i=last+1){
last=min(n/(n/i),m/(m/i));
ans+=(n/i)*(m/i)*(sum[last]-sum[i-1]);
}
return ans;
}
int t;
int main(){
scanf("%d",&t);
getmu();
pos(i,1,t){
scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
printf("%d\n",getans(b,d)-getans(a-1,d)-getans(b,c-1)+getans(a-1,c-1));
}
return 0;
}
原文:http://www.cnblogs.com/Hallmeow/p/7994929.html