羊车门问题

问题是这样的：有3扇关闭的门，一扇门后面停着汽车，其余门后是山羊，只有主持人知道每扇门后面是什么。参赛者可以选择一扇门，在开启它之前，主持人会开启另外一扇门，露出门后的山羊，然后允许参赛者更换自己的选择。

最开始我们想的是主持人已经打开了一只羊，换不换只是在一只羊和一辆车中选择，换不换的概率都是1/2，就觉得换不换都一样。

我们认真分析一下参赛者更换选择能得到车的概率

情况一：参赛者直接选中车门的概率是1/3，如果参赛者在已经选择车门的情况下更换，那么他得奖的可能性为0，根据条件概率公式：1/3*0=0；

情况二：参赛者直接选择羊门的概率是2/3，如果参赛者在已经选择车门的情况下更换，那么他得奖的可能性为1，根据条件概率公式：2/3*1=2/3。

结果：根据全概率公式为0+2/3=2/3，所以听主持人的更换选择得倒车的概率比较大。

from random import randint

n = eval(input("请输入样本的数量："))

a = 0 #不换的可能数
b = 0 #换的可能数

for i in range(n):
    car = randint(1, 3)           #车子所在门
    my  = randint(1, 3)           #自己选择的门
    if my == car:                 #第一次选中的情况
        a += 1
    else:                  
        b += 1  

result1 = a / n       
result2 = b / n      
print("更改选择的情况的可能性为{},不更改选择的可能性为{}".format(result2,result1))

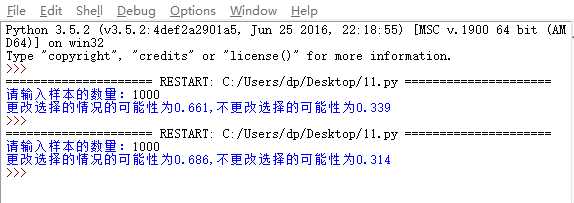
运行结果：

结组成员：吴铭贤 李凯旋

羊车门问题

原文：http://www.cnblogs.com/wyomissing/p/7725528.html