7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16Sample Output
228
题意 : 求一堆矩形的周长并,覆盖的的地方周长不计算
思路 : 类似于矩形的周长并 , 只不过不算面积 , 同时线段树中要多维护一个竖边的个数 。
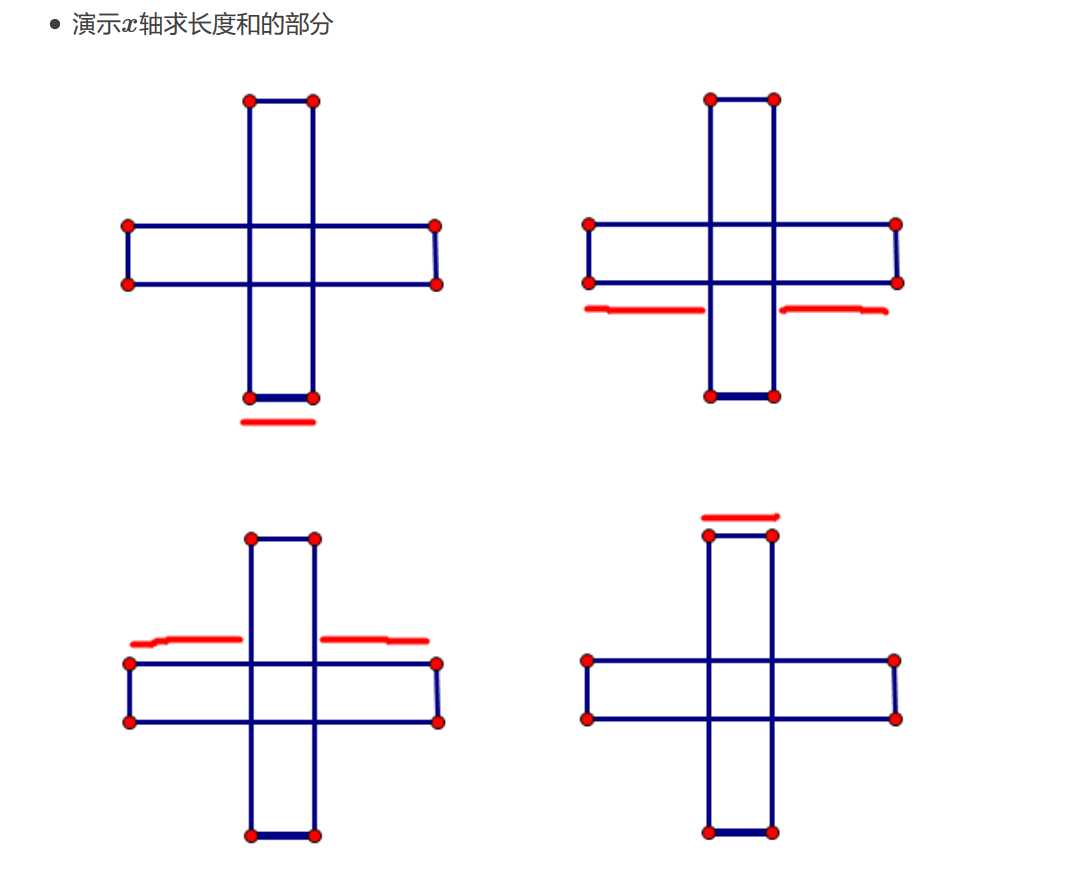
怎么求 图示的红线部分的变呢 ? 就是当前的边的长度 - 上一次边的长度。 好好理解下 。
还有一个很重要的地方是 就是判断两条边是否重叠或相交 好好理解下子 。
代码示例 :
/*
* Author: ry
* Created Time: 2017/10/24 11:11:20
* File Name: 1.cpp
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <string>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <time.h>
using namespace std;
const int eps = 1e4+5;
const double pi = acos(-1.0);
const int inf = 0x3f3f3f3f;
#define Max(a,b) a>b?a:b
#define Min(a,b) a>b?b:a
#define ll long long
struct seg
{
int l, r, h;
int f;
}po[eps];
int x[eps];
bool cmp(seg a, seg b){
return a.h < b.h;
}
struct node
{
int l, r, len, f;
int lf, rf, num;
}tree[eps<<2];
void build(int l, int r, int k){
tree[k].l = l;
tree[k].r = r;
tree[k].f = 0;
tree[k].len = tree[k].num = 0;
tree[k].lf = tree[k].rf = 0;
if (l == r) return;
int m = (l + r) >> 1;
build(l, m, k<<1);
build(m+1, r, k<<1|1);
}
void down(int k){
if (tree[k].f) {
tree[k].len = x[tree[k].r+1] - x[tree[k].l];
tree[k].lf = tree[k].rf = 1;
tree[k].num = 1;
}
else if (tree[k].l == tree[k].r){
tree[k].len = 0;
tree[k].lf = tree[k].rf = 0;
tree[k].num = 0;
}
else {
tree[k].len = tree[k<<1].len + tree[k<<1|1].len;
tree[k].lf = tree[k<<1].lf;
tree[k].rf = tree[k<<1|1].rf;
tree[k].num = tree[k<<1].num + tree[k<<1|1].num - (tree[k<<1].rf&&tree[k<<1|1].lf);
}
}
void update(int l, int r, int k, int pt){
if (l <= tree[k].l && tree[k].r <= r){
tree[k].f += pt;
down(k);
return;
}
int m = (tree[k].l + tree[k].r) >> 1;
if (l <= m) update(l, r, k<<1, pt);
if (r > m) update(l, r, k<<1|1, pt);
down(k);
}
int main() {
int n;
int a, b, c, d;
while (~scanf("%d", &n)){
int k = 1;
for(int i = 0; i < n; i++){
scanf("%d%d%d%d", &a, &b, &c, &d);
po[k].l = po[k+1].l = a;
po[k].r = po[k+1].r = c;
po[k].h = b, po[k+1].h = d;
po[k].f = 1, po[k+1].f = -1;
x[k] = a, x[k+1] = c;
k += 2;
}
sort(x+1, x+k);
sort(po+1, po+k, cmp);
int t = 2;
for(int i = 2; i < k; i++){
if (x[i] != x[i-1]) x[t++] = x[i];
}
build(1, t-1, 1);
int ans = 0, last = 0;
po[k].h = po[k-1].h
; for(int i = 1; i < k; i++){
int l = lower_bound(x+1, x+t, po[i].l) - x;
int r = lower_bound(x+1, x+t, po[i].r) - x - 1;
update(l, r, 1, po[i].f);
ans += 2*tree[1].num*(po[i+1].h - po[i].h);
ans += fabs((tree[1].len - last));
last = tree[1].len;
}
printf("%d\n", ans);
}
return 0;
}
原文:http://www.cnblogs.com/ccut-ry/p/7722928.html