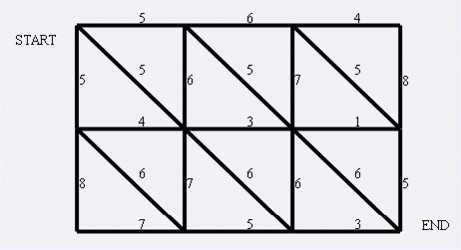
左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路
1:(x,y)<==>(x+1,y)
2:(x,y)<==>(x,y+1)
3:(x,y)<==>(x+1,y+1)
道路上的权值表示这条路上最多能够通过的兔子数,道路是无向的. 左上角和右下角为兔子的两个窝,
开始时所有的兔子都聚集在左上角(1,1)的窝里,现在它们要跑到右下解(N,M)的窝中去,狼王开始伏击
这些兔子.当然为了保险起见,如果一条道路上最多通过的兔子数为K,狼王需要安排同样数量的K只狼,
才能完全封锁这条道路,你需要帮助狼王安排一个伏击方案,使得在将兔子一网打尽的前提下,参与的
狼的数量要最小。因为狼还要去找喜羊羊麻烦.
2. Input
第一行为N,M.表示网格的大小,N,M均小于等于1000.
接下来分三部分
第一部分共N行,每行M-1个数,表示横向道路的权值.
第二部分共N-1行,每行M个数,表示纵向道路的权值.
第三部分共N-1行,每行M-1个数,表示斜向道路的权值.
输入文件保证不超过10M
3. Output
输出一个整数,表示参与伏击的狼的最小数量.
4. Sample Input
3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6
5. Sample Output
5. 思路
读了题后的第一反应是欢喜地打了个EK求最小割,然后就TLE了。
然后去读了一下题解,发现里面都提到了把题目转化为对偶图中的最短路。之前并不知道有这种操作,便去更加深入地了解了一下,发现真的很神奇!(可惜只适用于平面图)
改算法的思路大概是这样的:
将平面图上的每一个“面”转化为一个点,并在它们之间连边。显而易见地,每一条新连接的边都会和原图的一条边相交,与之相交的原图的边的容量便是该边的边权。最后将源点和汇点之间连一条边使得图的外部被分为两个平面,分别作为对偶图的起点和终点。此时很明显原图的最小割已经被转化为对偶图上的最短路了。最短路的距离可以通过各种算法实现,例如 Dijkestra。
下面的图也许可以帮助更好地理解:
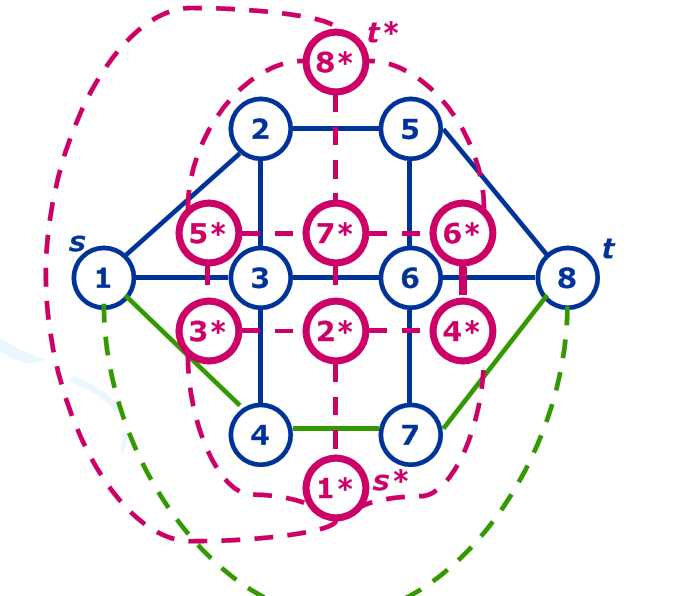
另外推荐阅读周冬的《浅析最大最小定理在信息学竞赛中的应用》,里面也有很详细的解释。
6. 代码
参看http://www.cnblogs.com/jimzeng/p/bzoj1001.html

