利用Logistic回归进行分类的思想就是:根据现有数据对分类边界线建立回归公式,以此进行分类。该算法最重要的就是要找到最佳拟合参数集。
本文介绍二值型输出分类器的数学原理。
针对这类问题:接收输入,输出为两个类别,这里假设为0和1,具有这样性质,且数学上容易处理的函数,有Sigmoid函数(S形函数)。
首先加载数据集:
def loadDataSet():
dataMat = []
labelMat = []
fr = open(‘/Users/Desktop/testSet.txt‘)
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) # 1.0 为常数项
labelMat.append(int(lineArr[2]))
return dataMat,labelMat
S形函数,输入为inX,输出为计算后的值,属于区间(0,1)
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
梯度下降(批处理)用python代码实现
def gradAscent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) # 转化为Numpy矩阵,方便计算
labelMatix = np.mat(classLabels).transpose()
m,n = np.shape(dataMatrix) # mxn
alpha = 0.001 # 设置步长
maxCycles = 500 # 迭代次数
weights = np.ones((n,1)) # 参数初始化为1(列向量 n)
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights) # mx1
error = (labelMatix - h) # mx1
weights = weights + alpha * dataMatrix.transpose() * error
return weights
下面用python的matplotlib画出决策边界,确定不同类别数据之间的分隔线:
def plotBestFit(weights):
dataMat, labelMat = loadDataSet()
dataArr = np.array(dataMat)
n = np.shape(dataArr)[0] # 数据集中数据的数量
xcord1 = []; ycord1 = []
xcord0 = []; ycord0 = []
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else:
xcord0.append(dataArr[i,1]); ycord0.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1,ycord1,s = 30,c = ‘red‘, marker=‘s‘)
ax.scatter(xcord0,ycord0,s = 30,c = ‘green‘)
x = np.arange(-3.0, 3.0, 0.1)
y = (- weights[0] - weights[1] * x) / weights[2]
ax.plot(x,y)
plt.xlabel(‘X1‘)
plt.ylabel(‘X2‘)
plt.show()
输出的图片如下:
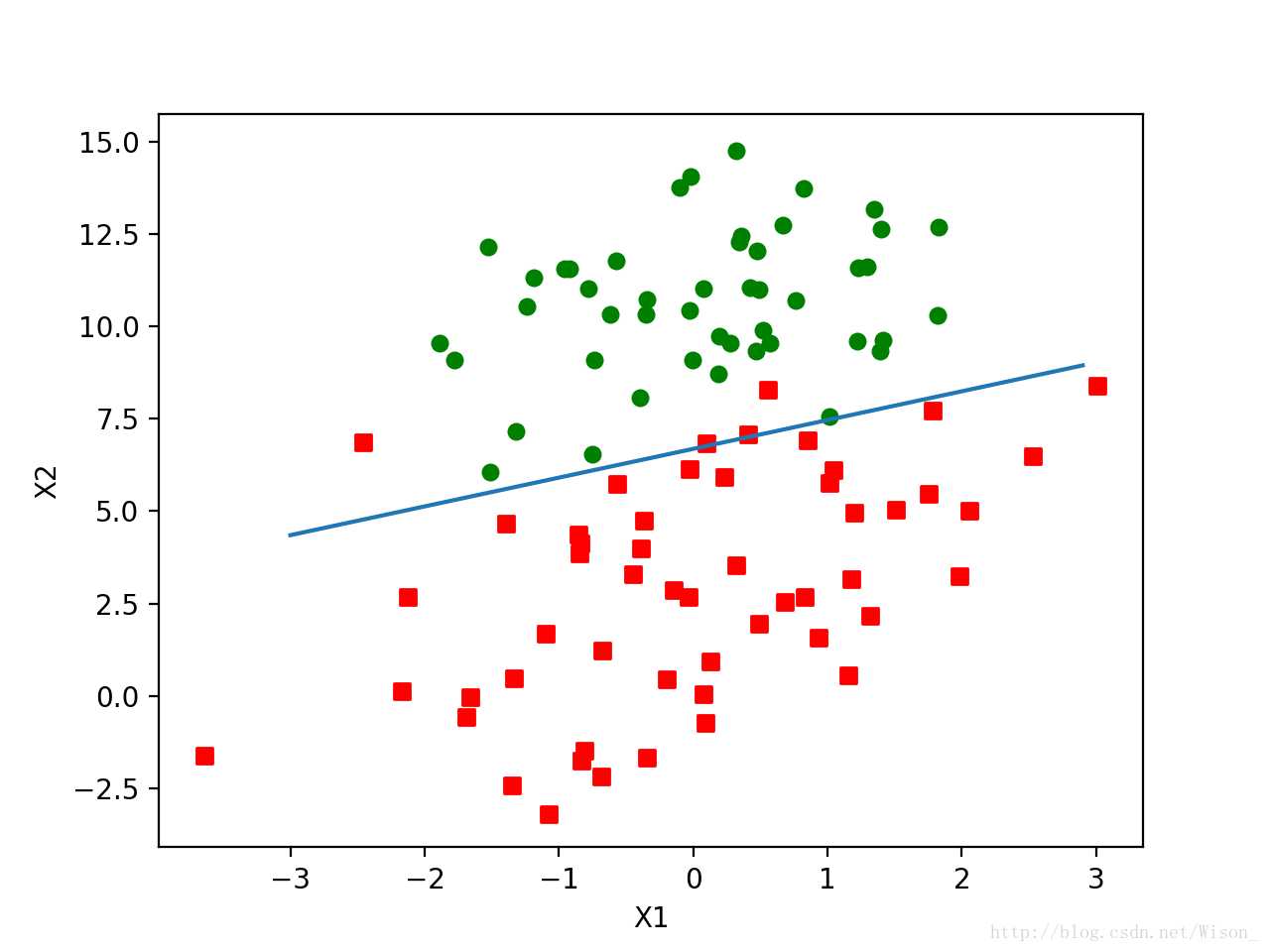
从上图可以看出分类的效果相当不错,但每次更新回归系数时都需要遍历整个数据集,当数据集相当庞大的时候计算量将不可想象。改进的方法是一次仅用一个样本点来更新回归系数,这种方法称为随机梯度上升算法,代码如下:
def stocGradAscent0(dataMatrix, classLabels):
m,n = np.shape(dataMatrix)
alpha = 0.01
weights = np.ones(n)
for i in range(m):
h = sigmoid(sum(dataMatrix[i] * weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights
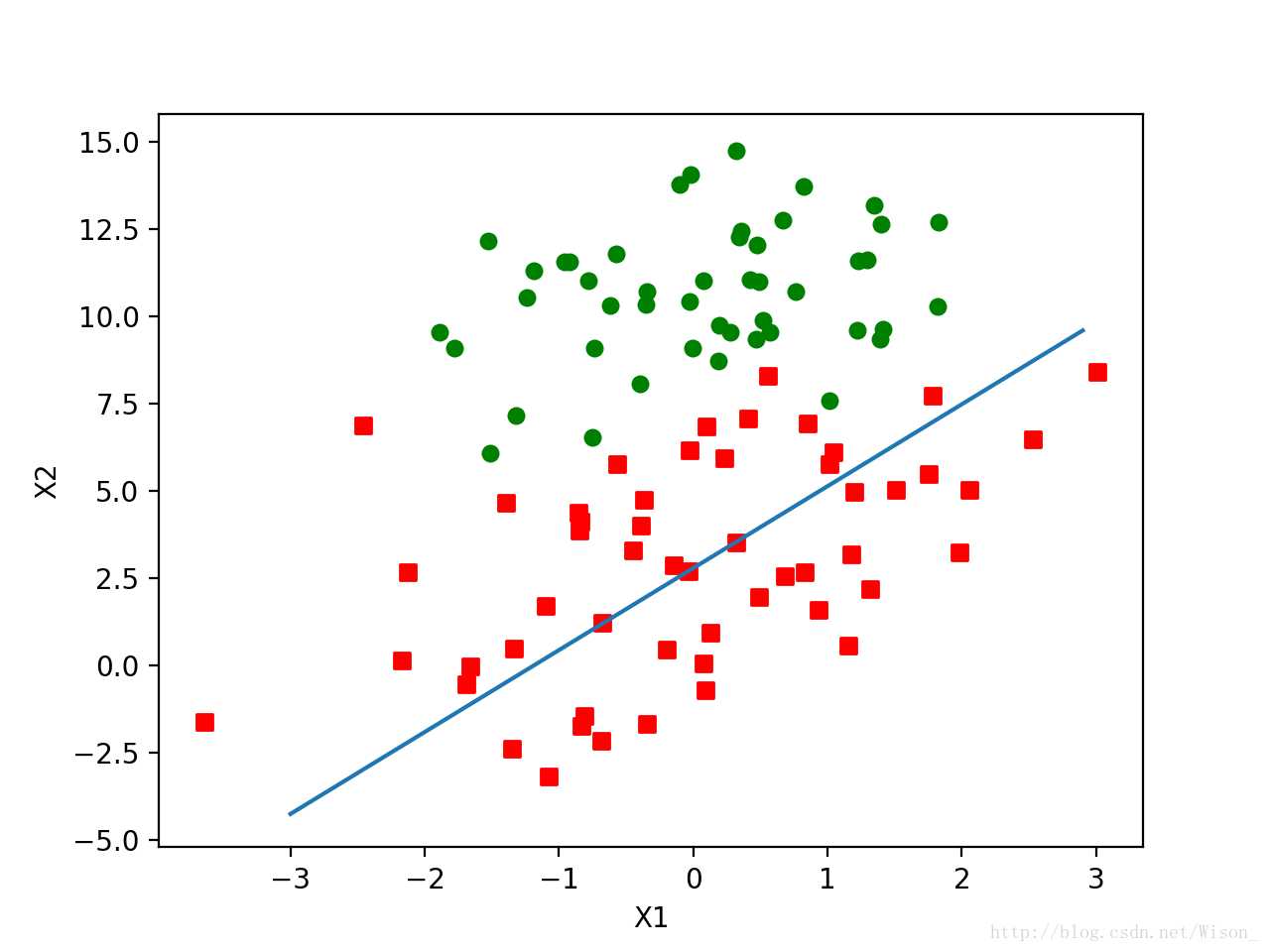
可以看出拟合的效果明显没有之前那么好,进而对随机梯度上升算法进一步做了如下优化:
# 改进的随机梯度上升算法
def stocGradAscent1(dataMatrix, classLabels, numIter = 150): # numIter为指定的迭代次数(针对整个数据集而言)
m,n = np.shape(dataMatrix)
weights = np.ones(n)
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4 /(1 + i + j) + 0.01 # 每次迭代调整alpha
randIndex = int(random.uniform(0,len(dataIndex))) # 随机选取样本更新回归系数,减少周期性波动
h = sigmoid(sum(dataMatrix[randIndex] * weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del(dataIndex[randIndex])
return weights
主要做了两处调整:
1> 每次迭代都会对步长alpha进行调整,虽然alpha会随着迭代次数增加不断变小,但永远不会减小到0,因为有一个常数项0.01,这是为了保证在多次迭代后新数据仍然具有一定的影响。
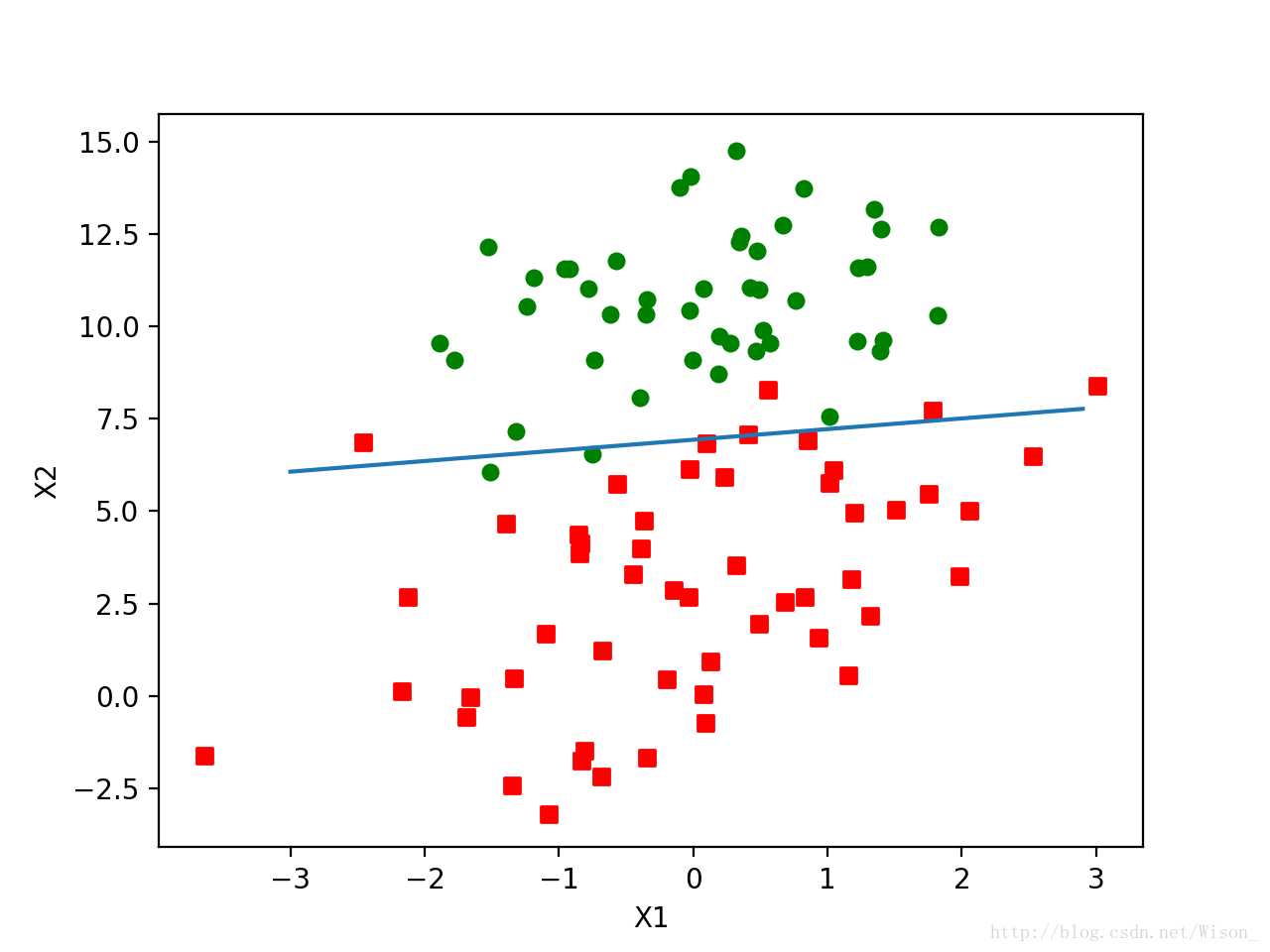
2> 为了减少周期性波动,随机选取样本来更新回归系数。 下面是改进后输出的图片,从图中可以看出分隔线达到了与批处理梯度下降差不多的效果,但所使用的计算量更少。
原文:http://www.cnblogs.com/weimusan/p/7499333.html