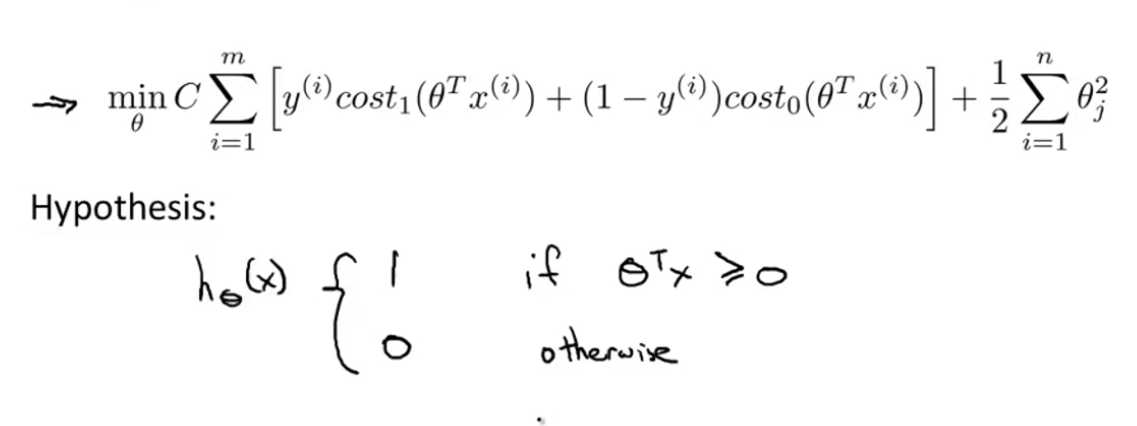Logistic回归的替代观点
J(θ)=-(yloghθ(x)+(1-y)log(1-hθ(x)))
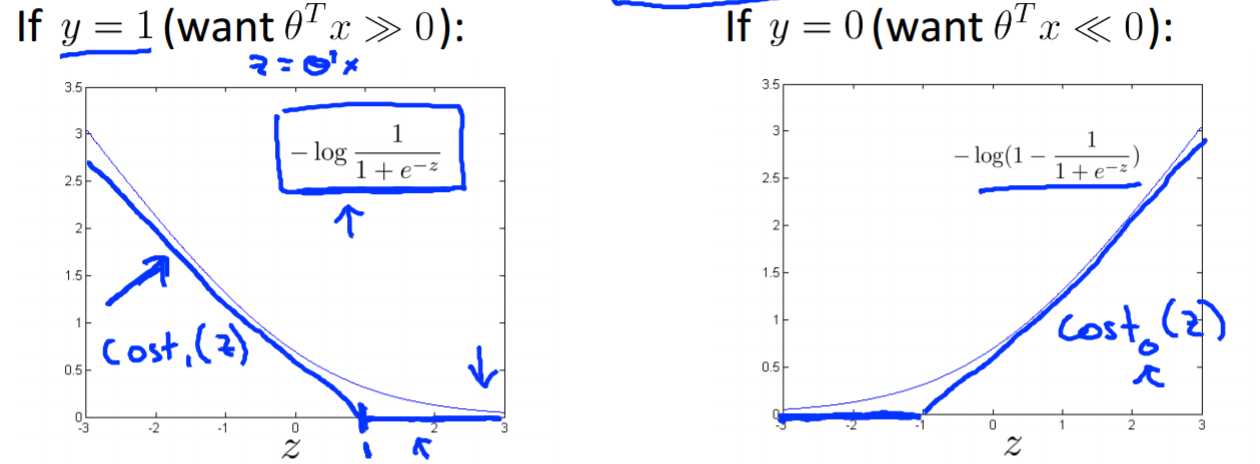
因为当Z足够大时,产生的误差几乎可以忽略不计。
所以我们用新的代价函数来代替逻辑回归的代价函数。
对比逻辑回归和支持向量机的代价函数:
支持向量机的预测函数:
大间距器:
在C很大的情况下,为了使代价函数减小,我们希望当y=1时,我们的z能大于等于1(不是仅仅大于等于0)
所以支持向量机的决策边界为:
大间距分类器的可视化
当C不是很大的时候可以忽略掉一些异常点
大间距分类器的数学原理
在C很大的情况下,为了使代价函数减小,代价函数变成
前缀近似等于0
假如分类边界为下图:
因为输入集在边界的投影长度较短,导致θ的范式距离较大
显然这使代价函数的值增大。
所以在C较大时我们得到以下的分类边界:
支持向量基
原文:http://www.cnblogs.com/zhengzhe/p/7410986.html