如题,给出一个网络图,以及其源点和汇点,求出其网络最大流。
输入输出格式
输入格式:
第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含三个正整数ui、vi、wi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi)
输出格式:
一行,包含一个正整数,即为该网络的最大流。
输入输出样例
输入样例#1:
4 5 4 3 4 2 30 4 3 20 2 3 20 2 1 30 1 3 40
输出样例#1:
50
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=25
对于70%的数据:N<=200,M<=1000
对于100%的数据:N<=10000,M<=100000
样例说明:
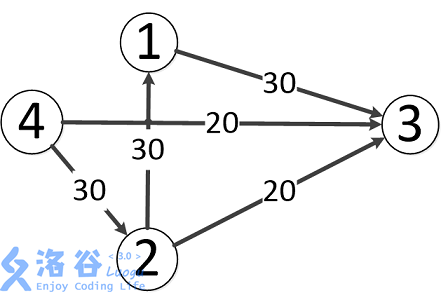
题目中存在3条路径:
4-->2-->3,该路线可通过20的流量
4-->3,可通过20的流量
4-->2-->1-->3,可通过10的流量(边4-->2之前已经耗费了20的流量)
故流量总计20+20+10=50。输出50。
一篇较好博文 :http://www.cnblogs.com/ShaneZhang/p/3755479.html
/*
网络最大流个人理解(并不透彻):
网络最大流是指网络中最大的可行流,可行流概念很好理解的。
增广路:简单来说就是指还可以有流量通过的路径。
求最大可行流可采用增广的算法:找出残量网络(还可增加流量),
即 容量-当前流量 和 一种逆向边(疑惑:逆向边 v-u的流量指u-v的初始当前流量还是0??) 所构成的网络,
每次找出增广路中的可行流量的min,将此增广路上的边进行增广(+min),直到不存在增广路。
至于建立逆向边(并不十分理解)才会使得已经增加了的流量回退,从而找到更大的可行流
(只要流量在满足网络流概念的情况下增加,则此时的网络中存在的一定是 更 优解)。
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
#include<algorithm>
#define ll long long
using namespace std;
const int N=300001;
const int maxn=0x7fffff;
inline int read()
{
int x=0;char c=getchar();
while(c<‘0‘||c>‘9‘)c=getchar();
while(c>=‘0‘&&c<=‘9‘)x=x*10+c-‘0‘,c=getchar();
return x;
}
int head[N],dis[N];
bool vis[N];
int now=0;
int n,m,S,T;
struct node{
int u,v,cap,flow,nxt;
}E[N];
inline void add(int u,int v,int w)
{
E[now].u=u;
E[now].v=v;
E[now].cap=w;
E[now].flow=0;
E[now].nxt=head[u];
head[u]=now++;
}
bool bfs(int start,int endd)
{
for(int i=1;i<=n;i++)
dis[i]=-1;
queue<int>Q;
Q.push(start);
dis[start]=0;
while(!Q.empty())
{
int topp=Q.front();
Q.pop();
for(int i=head[topp];~i;i=E[i].nxt)
{
if(dis[E[i].v]==-1&&E[i].cap>E[i].flow)
{
vis[E[i].v]=1;
dis[E[i].v]=dis[topp]+1;
Q.push(E[i].v);
}
}
}
if(dis[endd]==-1)
return 0;
return 1;
}
int dfs(int start,int minn)
{
if(start==T||minn<=0)
return minn;
int flow=0,f;
for(int i=head[start];~i;i=E[i].nxt)
{
if(dis[start]+1==dis[E[i].v]&&E[i].cap-E[i].flow>0)
{
f=dfs(E[i].v,min(minn,E[i].cap-E[i].flow));
E[i].flow+=f;
E[i^1].flow-=f;
flow+=f;
minn-=f;
if(minn<=0)
break;
}
}
return flow;
}
inline void Dinic(int S,int T)
{
int ansflow=0;
while(bfs(S,T))
ansflow+=dfs(S,maxn);
printf("%d",ansflow);
}
int main()
{
n=read(),m=read(),S=read(),T=read();
for(int i=1;i<=n;i++)
head[i]=-1;
for(int i=1;i<=m;i++)
{
int u=read(),v=read(),w=read();
add(u,v,w);
add(v,u,0);
}
Dinic(S,T);
return 0;
}
