【SinGuLaRiTy-1024】 Copyright (c) SinGuLaRiTy 2017. All Rights Reserved.
杂货店出售一种由N(3<=N<=12)种不同颜色的颜料,每种一瓶(50ML),组成的颜料套装。你现在需要使用这N种颜料;不但如此,你还需要一定数量的灰色颜料。杂货店从来不出售灰色颜料——也就是它不属于这N种之一。幸运的是,灰色颜料是比较好配置的,如果你取出三种不同颜色的颜料各x ml,混合起来就可以得到x ml的灰色颜料(注意不是3x)。
现在,你知道每种颜料各需要多少ml。你决定买尽可能少的“颜料套装”,来满足你需要的这N+1种颜料。那么你最少需要买多少个套装呢?
输入包含若干组测试数据。每组数据一行:第一个数N, 3<=N<=12, 含义如上;接下来N+1个数,分别表示你需要的N+1种颜料的毫升数。最后一种是灰色。所有输入的毫升数<=1000.
注意:输入中不存在每个颜料套装的毫升数。由题意可知,每种各50ml,即一共50N ml。
对于每一组数据,输出一个整数,表示最少套数。
| 样例输入 | 样例输出 |
3 40 95 21 0
7 25 60 400 250 0 60 0 500
4 90 95 75 95 10
4 90 95 75 95 11
5 0 0 0 0 0 333
0
|
2
8
2
3
4
|
样例的前四组数据,都很简单,直接找最大,然后模拟就可以,没什么好说的。但对于第五组数据,就有点坑了。我们会发现:如果按照常规解法一次50ml地配灰色颜料,答案显然不是4.因此,在这里我们要1ml、1ml地配,直到配满灰色的为止。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=15;
int a[maxn],b[maxn];
bool cmp(int a,int b)
{
return a>b;
}
int main()
{
int n,m,k;
while(scanf("%d",&n)&&n)
{
for(int i=0;i<n;i++)
scanf("%d",&a[i]);
scanf("%d",&m);
sort(a,a+n);
if(a[n-1]%50==0) k=a[n-1]/50;
else k=a[n-1]/50+1;
int t=0;
for(int i=0;i<n;i++)
b[i]=k*50-a[i];
while(t<m)
{
if(b[2]==0)
{
k+=1;
for(int i=0;i<n;i++)
b[i]+=50;
}
else
{
t++;
b[0]--,b[1]--,b[2]--;
sort(b,b+n,cmp);
}
}
cout<<k<<endl;
}
return 0;
}
任务规定,一个酸奶制造厂,在N (1 <= N <= 10,000) 个星期内,分别要向外提供Y[i] (0 <= Y_i <= 10,000)单位的酸奶。已知这个制造厂第i周制造每单位酸奶的费用为C[i] (1 <= C_i <= 5,000),储存室储存每1单位酸奶1星期的费用为S (1 <= S <= 100) 。问要完成这个任务的最小费用是多少。
第一行:两个整数N和S
第2~n+1行:第i+1行包含两个整数C[i]和Y[i]
一个整数,表示满足安排的最小花费。注意:这个数可能会超过32位整型。
| 样例输入 | 样例输出 |
4 5
88 200
89 400
97 300
91 500
|
126900
|
贪心。对于每一周的订单,维护最小花费:min_cost=min(C[i],min_cost+S)。
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#include<cstdio>
#include<iostream>
#define LL long long
#define MAXN 10010
#define INF 0x3f3f3f3f
using namespace std;
LL C[MAXN];
LL Y[MAXN];
LL cost;
int main()
{
int MAX=INF;
int N,S;
scanf("%d%d",&N,&S);
for(int i=1;i<=N;i++)
{
cin>>C[i]>>Y[i];
if(C[i]>MAX+S)
C[i]=MAX+S;
MAX=C[i];
cost+=C[i]*Y[i];
}
cout<<cost;
return 0;
}
将一个区域分成r*c个方块,每个方块有有一个海拔(可正可负)。求当给区域注入指定容量的水时,水面的海拔是多少,以及被水淹没的方块占总方块数的百分比。每个方块的面积为100m^2,水的容量单位为立方米。
多组用例,每组用例第一行为两个整数r和c表示区域行列数,然后是一个r*c的矩阵,矩阵元素为对应区域方块的海拔,最后是注入水的体积,以r=c=0结束输入
对于每组用例,输出注入水后水面的海拔以及被水淹没方块占总方块数的百分比
| 样例输入 | 样例输出 |
3 3
25 37 45
51 12 34
94 83 27
10000
0 0
|
Region 1
Water level is 46.67 meters.
66.67 percent of the region is under water.
|
(Tips: 如果在POJ上一直莫名TLE,WA,RE,建议把默认语言的G++换成C++,玄学......)
看到这道题,首先要明白这个r*c的区域和矩阵一点关系都没有,于是果断改成一列的一维数组。此时又发现体积并不好算,于是来一个sort,此时的区域就变成了如图-1所示的样子。现在,问题就比较简单了:对于每一组数据,我们只需要判断水面从左到右延伸到了哪一个位置就能判断覆盖方块数了(在每一个位置都有一个体积范围)。而对于体积,运用小学的体积公式也就搞出来了。(注意浮点数精度误差)
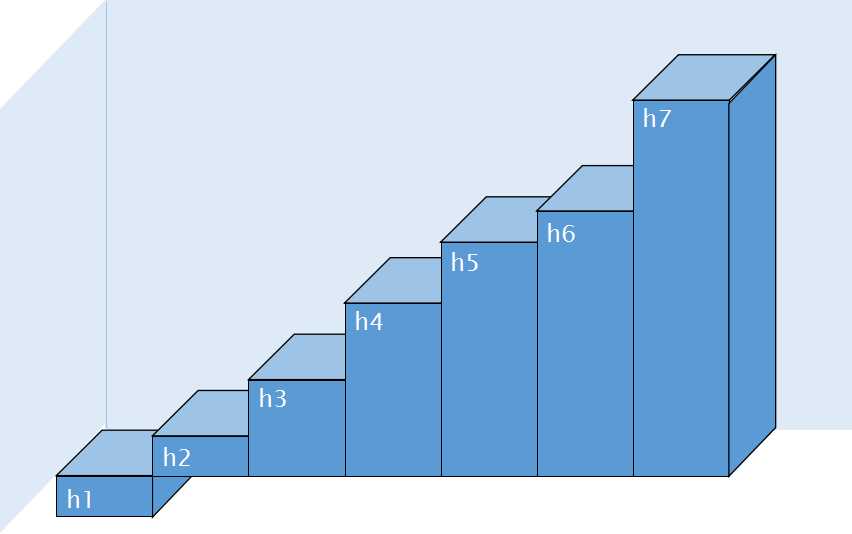
图-1
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
using namespace std;
int n,m,T;
int i;
double v;
double land[1000];
int main()
{
T=1;
while(scanf("%d%d",&n,&m)!=EOF)
{
if(m==0&&n==0)
return 0;
for(i=0;i<n*m;i++)
cin>>land[i];
cin>>v;
sort(land,land+n*m);
for(i=0;i<n*m-1;i++)
{
if(v<(land[i+1]-land[i])*(i+1)*100)
break;
v-=(land[i+1]-land[i])*(i+1)*100;
}
double h=land[i]+v/(i+1)/100;
if(v==0)
h=1;
printf("Region %d\n",T++);
printf("Water level is %.2f meters.\n",h);
printf("%.2f percent of the region is under water.\n",(i+1)/((double)(n*m))*100);
printf("\n");
}
return 0;
}
我们假设海岸是无限延伸的直线,陆地在海岸的一边,大海在另一边。每个小岛是一个点位于大海那一片区域。详见图片;每一个雷达的安装位置只能够在海岸线上,只能够覆盖半径为 d 的圆形区域。所以,如果小岛与雷达距离小于等于d才能够覆盖。我们可以用笛卡尔积坐标系,定义海岸线是 x轴,大海在x 上方,陆地在x 轴下方,给你每个小岛在大海中的位置,并且给出雷达的覆盖范围 d ,你的任务是写一个程序,找到最少需要安装的雷达数量且能够覆盖所有的小岛。一个位置表示(x,y)坐标。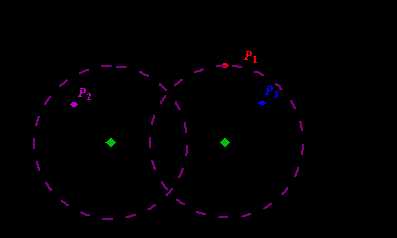
Figure A Sample Input of Radar Installations
输入是多组语句输入; 每行包含两个数 n 和 d:n 代表小岛的数量,d 代表雷达的覆盖半径;接下来n行是小岛的位置,用一个二维坐标来表示Xi,Yi; 当输入的 n 和 d 都为0,程序结束。 对于每组数据输出一个答案,每个答案占一行,输出最小需要的雷达数量,如果不能够满足要求,则输出 -1。| 样例输入 | 样例输出 |
3 2 1 2 -3 1 2 1 1 2 0 2 0 0 |
Case 1: 2 Case 2: 1 |
首先,我们将岛屿从左到右(x坐标从小到大)进行排序。接下来,我们走一遍循环,计算出能覆盖第i个岛屿的雷达的坐标范围 [ll[1],rr[1]] (相当于是x轴上的线段) ,如图-2。接下来,我们从左到右再走一次循环,这一次,我们看这些一段段线段有多少重合区域(这意味着有些岛屿可共用一个雷达),最后统计,求出答案。
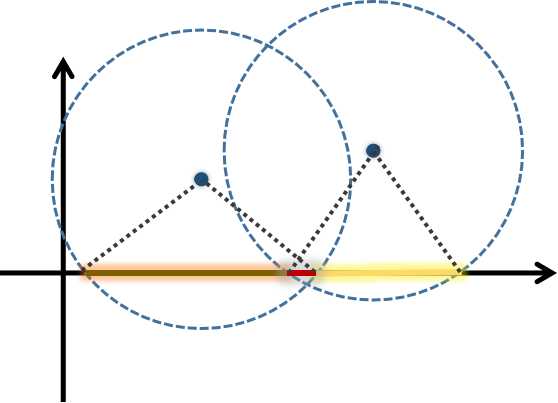
图-2
#include<iostream> #include<cstring> #include<cmath> #include<cstdio> using namespace std; double x[10000],y[10000],ll[11000],rr[10000]; int main() { int n,d; int cnt=1; while(cin>>n>>d) { if(n==0&&d==0) break; int flag=1,sum=1; for(int i=0;i<n;i++) { cin>>x[i]>>y[i]; if(y[i]>d) flag=0; } cout<<"Case "<<cnt; cnt++; if(flag==0||d==0) { cout<<": -1"<<endl; continue; } int t; for(int i=0;i<n-1;i++) { for(int j=0;j<n-i-1;j++) { if(x[j]>x[j+1]) { t=x[j]; x[j]=x[j+1]; x[j+1]=t; t=y[j]; y[j]=y[j+1]; y[j+1]=t; } } } for (int i=0;i<n;i++) { double s=sqrt(d*d-y[i]*y[i]); ll[i]=x[i]-s; rr[i]=x[i]+s; } double x=rr[0]; for(int i=1;i<n;i++) { if(ll[i]>x) { x=rr[i]; sum++; } if(rr[i]<x) { x=rr[i]; } } cout<<": "<<sum<<endl; } return 0; }
Pizoor Communications Inc.要建立一套通信系统,该通信系统需要n种设备,而每种设备分别可以有m1、m2、m3、...、mn个厂家提供生产,而每个厂家生产的同种设备都会存在两个方面的差别:带宽bandwidths 和 价格prices。
现在每种设备都各需要1个,考虑到性价比问题,要求所挑选出来的n件设备,要使得B/P最大。其中B为这n件设备的带宽的最小值,P为这n件设备的总价。
第一行包含一个整数t (1 ≤ t ≤ 10),表示有t组数据。
每组数据的第一行包含一个整数n (1 ≤ n ≤ 100),表示所需的设备种类数。接下来有n行,其中第i (1 ≤ i ≤ n)行的第一个整数mi (1 ≤ mi ≤ 100)表示生产第i种设备的厂家数量,接下来在同一行有两两成对的整数,第一个表示带宽,第二个表示价格。
输出对于每一组数据而言的B/P的最大值,保留三位小数。
| 样例输入 | 样例输出 |
1 3
3 100 25 150 35 80 25
2 120 80 155 40
2 100 100 120 110
|
0.649
|
本来听说这道题是一道DP题,但考虑到这是贪心复习,还是用贪心+剪枝吧。
从最小带宽开始枚举,用贪心法选出带宽大于等于最小带宽的最低价格;然后再比较更新最大的(B/P)的值,直到到达最大带宽;如果从带宽枚举上去,一定符合要求。
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
const int Max=101;
struct node
{
double b;
double p;
};
node a[Max][Max];
double b[Max*Max];
int m[Max];
int bsize;
int cmp(const void *a,const void *b)
{
return (*(double *)a)-(*(double *)b);
}
int main()
{
int t,n;
cin>>t;
while (t--)
{
memset(a,0,sizeof(a));
memset(m,0,sizeof(m));
cin>>n;
int i,j,k;
int bsize=0;
for (i=0;i<n;i++)
{
cin>>m[i];
for (j=0;j<m[i];j++)
{
cin>>a[i][j].b>>a[i][j].p;
b[bsize++]=a[i][j].b;
}
}
qsort(b,bsize,sizeof(b[0]),cmp);
double mmax=0;
double mmin;
double sump=0;
double temp=0;
for (i=0;i<=bsize-1;i++)
{
sump=0;
int changFlag = 0;
for (j=0;j<n;j++)
{
mmin=32767;
for (k=0;k<m[j];k++)
{
if (a[j][k].b>=b[i]&&a[j][k].p<mmin)
{
mmin=a[j][k].p;
changFlag = 1;
}
}
sump+=mmin;
}
if(!changFlag)
break;
temp=b[i]*1.0/sump;
if(temp>mmax)
mmax=temp;
}
printf("%.3lf\n",mmax);
}
return 0;
}
ACM公司租用的楼层如下图所示:

这层楼的两端各有200个房间。现在公司决定在房间之间转移桌子。在移动过程中,有且仅有一张桌子能够在过道内。因此,ACM公司需要一种高效的安排来搬运桌子。已知,将一张桌子从一个房间移到另一个房间需要不到10分钟。由于将桌子从房间i到房间j移动的过程中,仅需使用过道中的i~j的部分。若两个桌子的移动不共同使用同一段过道,就可以同时进行。例如下表所示:

对于每一个房间而言,仅有一张桌子可以被移进或移出。你的任务是写一个程序来帮助计算所需的最少时间。
输入包含T组数据。
对于每一组数据,第一行包含一个整数N (1 <= N <= 200),表示需要移动的桌子。接下来有N行,每行两个整数s和t,表示桌子从s移动到t。
对于每一组数据,输出完成移动所需的最少时间。
| 样例输入 | 样例输出 |
3
4
10 20
30 40
50 60
70 80
2
1 3
2 200
3
10 100
20 80
30 50
|
10
20
30
|
只需把区间经过的地方计数,最后找到最大计数就可以了。答案的最优性说明:题意可以用区间图表示,即每一个区间为一个顶点,如果两个区间范围相交,则在其间连上一条边。题目便转化为求区间图的色数,由定理:区间图中色数=团数知道求最大团的顶点数即可。那么最大团的顶点数就是上述思路。[最大团是什么?]
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define N 202
using namespace std;
int n,flag[N],T;
int main()
{
scanf("%d",&T);
while(T--)
{
int a,b,res=0;
scanf("%d",&n);
memset(flag,0,sizeof(flag));
for(int i=0;i<n;i++)
{
scanf("%d %d",&a,&b);
if(a>b)
{
swap(a,b);
}
a=(a-1)>>1;
b=(b-1)>>1;
for(int j=a;j<=b;j++)
flag[j]++;
}
for(int i=0;i<N;i++)
res=max(res,flag[i]);
printf("%d\n",res*10);
}
return 0;
}
给出一个大于4的整数m和一个真分数a/b,求最佳素数对p、q,使得a/b<=p/q<=1且pq<=m。最佳即为满足条件的数对中pq最大的一对。
输入文件最多2000行。每一行包含了三个整数:整数m,分子a,分母b。( 4 < m <= 100000 and 1 <= a <= b <= 1000 且满足 0 < a / b < 1)
以三个0结尾。
输出是一个由正整数数对组成的序列。表示每一组数据中的p、q。
| 样例输入 | 样例输出 |
|
5 1 2
99999 999 999
1680 5 16
1970 1 1
2002 4 11
0 0 0
|
2 2
313 313
23 73
43 43
37 53
|
直接枚举查找:快速求出素数表后,运用二分查找检查当前数是否为素数。(注意,由于是求最大,所以从后往前搜,直到j<z时退出)。
还要关注p的取值范围:[1,sqrt(n)]
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
int prim[100005],is[100005];
int num=0;
int Find(int v)
{
int m;
int l=1,h=num;
while(l<h)
{
m=(l+h)/2;
if(prim[m]==v)
return 1;
if(prim[m]<v)
l=m+1;
else
h=m;
}
return 0;
}
int main()
{
int m,a,b,Max,j,i,x,zx,zi,z;
double t;
int s,e=(int)(sqrt(0.0+100000)+1);
memset(is,1,sizeof(is));
prim[++num]=2;
is[0]=is[1]=0;
for(i=4;i<=100000;i+=2)
is[i]=0;
for(i=3;i<e;i+=2)
if(is[i])
{
prim[++num]=i;
for(s=i*2,j=i*i;j<=100000;j+=s)
is[j]=0;
}
for(;i<100000;i+=2)
if(is[i])
prim[++num]=i;
while(scanf("%d%d%d",&m,&a,&b)!=EOF)
{
z=0;
if(m==0 && a==0 && b==0)
break;
t=a*1.0/b;
for(int j=m;j>=1;j--)
{
if(j<z)
break;
Max=(int)sqrt(0.0+j);
for(i=Max;i>=1;i--)
{
x=j/i;
if(x*t<=i && x>=i)
if(Find(i)&&Find(x))
if(x*i>z)
{
zx=x;
zi=i;
z=x*i;
}
}
}
printf("%d %d\n",zi,zx);
}
return 0;
}
鲍勃喜欢玩战略游戏。现在有一座城市,其内部的道路构成了一棵树。鲍勃可以在某些城市派一个士兵守护,该士兵可以瞭望到所有与该城市相连的边。问鲍勃最少要派遣多少个士兵,才能把所有的边都瞭望到。
例如,在下面这棵树中,只需要把士兵放在节点1就可以瞭望到左右的边了。
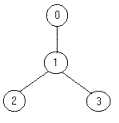
输入文件包含多组数据。
每一组数据包含了对树的以下描述:
1> 节点数N;
2> 接下来N行,每一行对一个节点进行具体描述,其格式如下:
节点编号:(与其连接的道路数m) 连接的节点1 连接的节点2 连接的节点3 ......连接的节点m
对于每一组数据,输出需要的最少士兵数。
| 样例输入 | 样例输出 |
|
4 |
1
2
|
最少点覆盖问题
可以用树形DP解决,我们把无根树抽象成一棵有根树,0为树根。对于任意一个节点i来说,设dp[i][0]表示在该节点不放士兵,dp[i][1]表示在该节点放置士兵。
那么结合他的子节点就可以得到状态转移方程
dp[i][1]=sum(dp[k][0])+1 k为i的子节点,下同,因为本节点没放,则子节点一定要放
dp[i][0]=sum(min(dp[k][0],dp[k][1])) 因为本节点放了,所以取子节点放和不放的最小值
最后答案就是min(dp[0][0],dp[0][1])
#include<iostream>
#include<vector>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int maxn = 1600;
int dp[maxn][2];
int n;
vector<int> tree[maxn];
int min(int a,int b)
{
return a<b?a:b;
}
void dfs(int fa,int now)
{
dp[now][0] = 0;
dp[now][1] = 1;
int len = tree[now].size();
int i;
for(i=0;i<len;i++)
{
int t=tree[now][i];
if(t!=fa)
{
dfs(now,t);
dp[now][0] += dp[t][1];
dp[now][1] += min(dp[t][0],dp[t][1]);
}
}
}
int main()
{
while(~scanf("%d",&n))
{
int i;
for(i=0;i<n;i++)
{
tree[i].clear();
}
for(i=0;i<n;i++)
{
int b;
int a;
int j;
scanf("%d:(%d)",&a,&b);
for(j=0;j<b;j++)
{
int x;
scanf("%d",&x);
tree[a].push_back(x);
tree[x].push_back(a);
}
}
dfs(-1,0);
cout<<min(dp[0][0],dp[0][1])<<endl;
}
return 0;
}
农夫约翰带着他的奶牛们去参加一个比赛。奶牛们排成一列,依次取出每头奶牛名字的首字母组成队名。为了得到一个字典序最小的队名。约翰要重新排列奶牛队伍,排列规则是这样的:他只能将奶牛队列的队头或队尾依次加入新队列的队尾,直到所有奶牛全部加入到新队列为止。问他能得到的字典序最小的队名?
第1行包含一个整数N,表示奶牛的总数量。
第2到N+1行描述每一头奶牛。第i+1行表示在原本序列中编号为i的奶牛的首字母。
字典序最小的字符串。
| 样例输入 | 样例输出 |
6
A
C
D
B
C
B
|
ABCBCD
|
贪心就行。每次从上和从下选择最小的,若相等则向中间搜索。
#include<cstdio>
#include<cstring>
#include<iostream>
#define MAXN 2010
using namespace std;
int n,str[MAXN];
int main()
{
scanf("%d",&n);
char ch;
for(int i=0;i<n;i++)
{
getchar();
ch=getchar();
str[i]=ch-‘A‘;
}
int pre=0,last=n-1,Count=0;
for(int i=0;i<n;i++)
{
if(str[pre]==str[last])
{
int pr=pre,la=last,flag=0;
while(pr<=la)
{
if(str[pr]<str[la])
{
printf("%c",str[pre]+‘A‘);
Count++;
flag=1;
pre++;
break;
}
else if(str[pr]>str[la])
{
printf("%c",str[last]+‘A‘);
Count++;
flag=1;
last--;
break;
}
pr++,la--;
}
if(!flag)
{
printf("%c",str[pre]+‘A‘);
Count++;
pre++;
}
}
else if(str[pre]<str[last])
{
printf("%c",str[pre]+‘A‘);
Count++;
pre++;
}
else
{
printf("%c",str[last]+‘A‘);
Count++;
last--;
}
if(Count==80)
{
Count=0;
printf("\n");
}
}
if(Count)
printf("\n");
return 0;
}
萨鲁曼要对自己的一列军队进行监视,因此他要赋予这一列军队中的部分士兵监视的权利。但每一个监视的士兵仅能覆盖距离自己R个单位以内的士兵(包括第R个)。现在,若要覆盖整支军队,至少需要多少个监视的士兵?
输入包含多组数据。每一组数据以两个整数R和N开始,R (0 ≤ R ≤ 1000)表示士兵能够监视的范围,N( 1 ≤ N ≤ 1000)表示这一列军队的士兵数。接下来一行包含N个整数,表示每一个士兵所处的位置X ( 1 ≤ X ≤ 1000)。当R=N=-1时,输入数据结束。
对于每一组数据,输出最少需要的士兵数。
| 样例输入 | 样例输出 |
0 3
10 20 20
10 7
70 30 1 7 15 20 50
-1 -1
|
2
4
|
从一个未覆盖的位置向前遍历,找到满足距离小于 R 的最右边的点,这个点一定作为一个装置的放置位置,然后从这个位置找到右边的最小的不能覆盖到的位置,这个位置作为下一次的起点...循环下去,直到所有的点都被覆盖到。
#include<cstring> #include<cstdlib> #include<cmath> #include<algorithm> #include<cstdio> #include<iostream> #define MAXN 1010 using namespace std; int army[MAXN]; int R,N; int main() { while(scanf("%d%d",&R,&N)!=EOF) { if(R==-1&&N==-1) return 0; for(int i=1;i<=N;i++) { scanf("%d",&army[i]); } sort(army+1,army+N+1); int i=1,cnt=0; while(i<=N) { int bg=army[i++]; while(i<=N&&army[i]<=bg+R) { i++; } int st=army[i-1]; while(i<=N&&army[i]<=st+R) { i++; } cnt+=1; } printf("%d\n",cnt); memset(army,0,sizeof(army)); } }
Farmer John要去做篱笆,他一共需要N块木板,也量出每块木板需要多长。他买了这么一整块木板,这个木板的长度是所有需要的木板长度之和。但是他没有锯子。于是他找朋友去借锯子。可是朋友要收费。收费是这样的,锯开一块长度为L的木板收费L元。请问Farmer John使用他朋友的锯子,最少要花多少钱。
第1行: 包含一个整数N (1 ≤ N ≤ 20,000) ,表示所需木板的数量。
第2到N+1行:每行一个整数,表示一块木板的长度L (1 ≤ L ≤ 50,000)。
一个整数,表示Farmer John最少花费的金额。
| 样例输入 | 样例输出 |
3
8
5
8
|
34
|
由于要使花费最小,因此很容易知道,我们每一次需要切掉最长的那一个部分,来防止那一部分在后面的计算中被反复叠加进花费中。当然,如果我们直接用sort排序的话,肯定会超时,所以我们要用优先队列。做这道题时总有种“合并果子”的感觉。
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<queue>
using namespace std;
priority_queue<int,vector<int>,greater<int> > pq;
int main()
{
int n(0);
cin>>n;
while(cin>>n)
{
pq.push(n);
}
long long sum(0);
int l1(0),l2(0);
while(pq.size()>1)
{
l1=pq.top();
pq.pop();
l2=pq.top();
pq.pop();
sum = sum+l1+l2;
pq.push(l1+l2);
}
cout<<sum;
return 0;
}
农夫约翰让他的N头奶牛们打扫谷仓。他把一天分成T个时间段,第一个时间段为1,最后一个时间段为T。第i头奶牛愿意从第Si个时间段工作到第Ti个时间段。问最少需要多少奶牛,才能保证每一个时间段都有奶牛在工作。如果不能保证,则输出-1.
第1行:两个整数N (1<= N <=25,000)和T (1<= T <=1,000,000)。
第2到N+1行:每一行包含一组开始时间和结束时间,表示一头奶牛工作的时间段。
输出一个整数,表示最少需要多少头奶牛。
| 样例输入 | 样例输出 |
3 10
1 7
3 6
6 10
|
2
|
这题乍一看,不就是区间覆盖问题吗? [CQBZOJ上的区间覆盖问题]
先对每一个时间段(其实就是线段)按左端点由小到大进行排序,从时间段1开始一段一段地接上来,连接时,在前后两条线段有交点的前提下使新的右端点最远,这样就能保证使用最少的线段,即奶牛数最小。
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = 25000 + 5;
const int maxd = 1000000 + 5;
struct Edge
{
int x;
int y;
}cow[maxn];
int N,T;
int X,Y;
bool cmp(Edge a,Edge b)
{
if(a.x==b.x) return a.y>b.y;
return a.x<b.x;
}
int main()
{
X=0;
Y=0;
scanf("%d%d",&N,&T);
for(int i=0;i<N;i++)
{
scanf("%d%d",&cow[i].x,&cow[i].y);
if(cow[i].x==1)
X=1;
if(cow[i].y==T)
Y=1;
}
sort(cow,cow+N,cmp);
if(X==0||Y==0)
{
printf("-1\n");
return 0;
}
int ans=1,End=0;
int Start=cow[0].y;
int maxy=cow[0].y;
while(true)
{
while(End+1<N&&cow[End+1].x<=Start+1)
{
End++;
if(cow[End].y>maxy)
{
maxy=cow[End].y;
}
}
if(maxy!=Start)
{
ans++;
Start=maxy;
}
else
{
if(End==N-1)
{
break;
}
else
{
printf("-1\n");
return 0;
}
}
}
printf("%d\n",ans);
return 0;
}
有N头奶牛,(1<=N<=50,000),每头奶牛只在特定的时间段内[A,B]内才愿意挤奶(1<=A,B<=1,000,000)。一个挤奶机只能同时挤一头奶牛。农夫约翰最少需要准备多少个挤奶机,才能满足所有奶牛的挤奶需求。
第1行:一个整数N,表示奶牛数。
第2到N+1行:每一行包含两个整数,分别表示一头奶牛愿意挤奶的开始时间和结束时间。
第1行:输出所需要的挤奶机的最少数量。
第2到N+1行:第i+1行的整数表示第i头奶牛所使用的挤奶机的编号。
| 样例输入 | 样例输出 |
5
1 10
2 4
3 6
5 8
4 7
|
4
1
2
3
2
4
|
<样例解释>
下面是挤奶机的时间安排表:(其它合理答案均可)
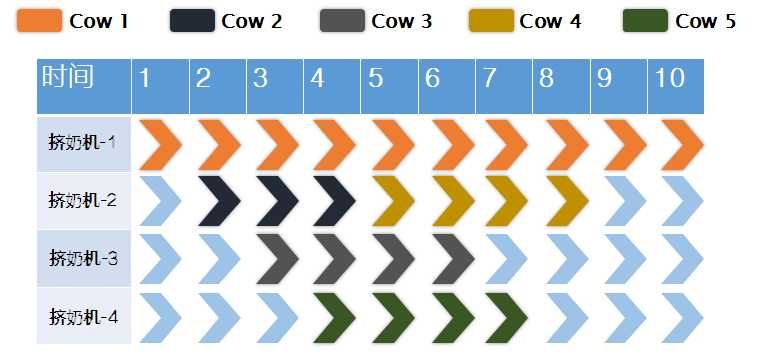
先按奶牛要求的时间起始点进行从小到大排序,然后维护一个优先队列,里面以已经开始挤奶的奶牛的结束时间早为优先。然后每次只需要检查当前是否有奶牛的挤奶工作已经完成的机器即可,若有,则换那台机器进行工作。若没有,则加一台新的机器。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
const int maxn=50000+10;
int order[maxn];
struct Node
{
int st,en,pos;
friend bool operator<(Node a,Node b)
{
if(a.en==b.en)
return a.st<b.st;
return a.en>b.en;
}
}node[maxn];
bool cmp(Node a,Node b)
{
if(a.st==b.st)
return a.en<b.en;
else
return a.st<b.st;
}
priority_queue<Node>Q;
int main()
{
int n,ans;
while(~scanf("%d",&n))
{
for(int i=1;i<=n;i++)
{
scanf("%d%d",&node[i].st,&node[i].en);
node[i].pos=i;
}
sort(node+1,node+1+n,cmp);
ans=1;
Q.push(node[1]);
order[node[1].pos]=1;
for(int i=2;i<=n;i++)
{
if(!Q.empty()&&Q.top().en<node[i].st)
{
order[node[i].pos]=order[Q.top().pos];
Q.pop();
}
else
{
ans++;
order[node[i].pos]=ans;
}
Q.push(node[i]);
}
printf("%d\n",ans);
for(int i=1;i<=n;i++)
printf("%d\n",order[i]);
while(!Q.empty()) Q.pop();
}
return 0;
}
一个整数,表示约翰付给贝茜津贴得最多的周数。
| 样例输入 | 样例输出 |
3 6
10 1
1 100
5 120
|
111
|
开始看到题目里的整除关系时,整个人是完全懵逼的:这是什么呀?后来想想也就想通了,这个条件实际上就是解题的关键。
对于面值大于C的硬币自然不用说。一枚用一周。
对于面值小于C的硬币。我们先考虑一个C的方案。要使用的周数最多我们应该就要使钱的利用率最大。也就是说损失的钱最少,尽量不要超过C太多。在不超过C的情况下对于大面值和小面值的优先使用大面值的。因为小面值的组合可得到大面值(整除关系)。留下小面值给后面的组合最优的可能性越大。如这种策略下没凑够C的话就找一个最小的面额。使得组合值大于C。(使损失值最小)
#include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> #include<cmath> const int INF=0x3f3f3f3f; using namespace std; struct node { int val,mou; }mon[25]; int n,c; int need[25]; bool cmp(node a,node b) { return a.val<b.val; } int main() { int i,ans,ti,rest,lim,mday; while(~scanf("%d%d",&n,&c)) { ans=0; lim=-1; for(i=0;i<n;i++) scanf("%d%d",&mon[i].val,&mon[i].mou); sort(mon,mon+n,cmp); for(i=n-1;i>=0;i--) if(mon[i].val>=c) ans+=mon[i].mou; else { lim=i; break; } while(1) { memset(need,0,sizeof need); rest=c; for(i=lim;i>=0;i--) { if(!mon[i].mou||!rest) continue; ti=rest/mon[i].val; ti=min(ti,mon[i].mou); need[i]=ti; rest-=ti*mon[i].val; } if(rest) { for(i=0;i<=lim;i++) { if(mon[i].val>=rest&&(mon[i].mou-need[i])) { need[i]++; rest=0; break; } } if(rest) break; } mday=INF; for(i=0;i<=lim;i++) if(need[i]) mday=min(mday,mon[i].mou/need[i]); ans+=mday; for(i=0;i<=lim;i++) mon[i].mou-=mday*need[i]; } printf("%d\n",ans); } return 0; }
Time: 2017-07-14
原文:http://www.cnblogs.com/SinGuLaRiTy2001/p/7158946.html