[codevs1002]搭桥
有一矩形区域的城市中建筑了若干建筑物,如果某两个单元格有一个点相联系,则它们属于同一座建筑物。现在想在这些建筑物之间搭建一些桥梁,其中桥梁只能沿着矩形的方格的边沿搭建,如下图城市1有5栋建筑物,可以搭建4座桥将建筑物联系起来。城市2有两座建筑物,但不能搭建桥梁将它们连接。城市3只有一座建筑物,城市4有3座建筑物,可以搭建一座桥梁联系两栋建筑物,但不能与第三座建筑物联系在一起。

在输入的数据中的第一行包含描述城市的两个整数r 和c, 分别代表从北到南、从东到西的城市大小(1 <= r <= 50 and 1 <= c <= 50). 接下来的r 行, 每一行由c 个(“#”)和(“.”)组成的字符. 每一个字符表示一个单元格。“#”表示建筑物,“.”表示空地。
在输出的数据中有两行,第一行表示建筑物的数目。第二行输出桥的数目和所有桥的总长度。
样例1
3 5
#...#
..#..
#...#
样例2
3 5
##...
.....
....#
样例3
3 5
#.###
#.#.#
###.#
样例4:
3 5
#.#..
.....
....#
样例1
5
4 4
样例2
2
0 0
样例3
1
0 0
样例4
3
1 1
试题分析:这个题我一开始看分类是搜索,并没有想到并查集……后来看了眼黄学长的博客,恍然大悟TAT
标程就是DFS+并查集
①用dfs联通块求第一问,然后把块标号
②枚举块的延伸,建立桥,排序路径长度(如图)
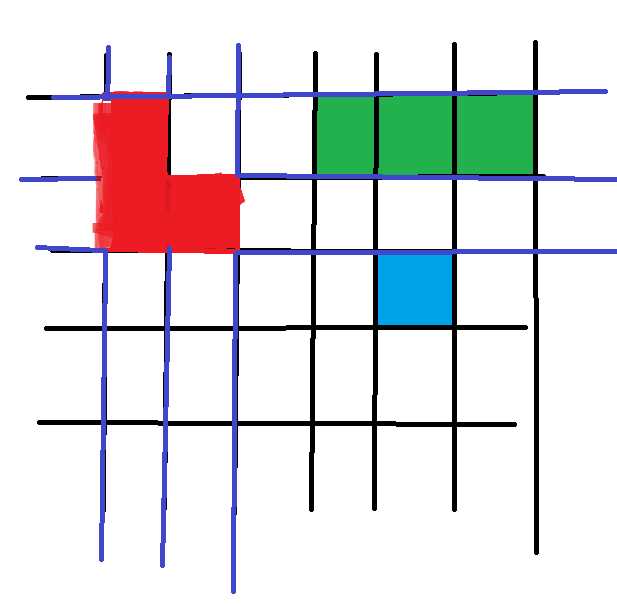
显然,在一个方格的一点,如果他向上延伸但是上面有块与他一个联通块,那么他就可以舍去
③merge并统计答案
代码
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#include<stack>
#include<vector>
#include<algorithm>
//#include<cmath>
using namespace std;
const int INF = 9999999;
#define LL long long
inline int read(){
int x=0,f=1;char c=getchar();
for(;!isdigit(c);c=getchar()) if(c==‘-‘) f=-1;
for(;isdigit(c);c=getchar()) x=x*10+c-‘0‘;
return x*f;
}
int N,M;
int Map[101][101];
char c;
int cnt;
int vis[52][52];
int dfsans1(int a,int b){
vis[a][b]=cnt+1;
if(Map[a-1][b]&&!vis[a-1][b]) dfsans1(a-1,b);
if(Map[a+1][b]&&!vis[a+1][b]) dfsans1(a+1,b);
if(Map[a][b-1]&&!vis[a][b-1]) dfsans1(a,b-1);
if(Map[a][b+1]&&!vis[a][b+1]) dfsans1(a,b+1);
if(Map[a-1][b+1]&&!vis[a-1][b+1]) dfsans1(a-1,b+1);
if(Map[a+1][b-1]&&!vis[a+1][b-1]) dfsans1(a+1,b-1);
if(Map[a+1][b+1]&&!vis[a+1][b+1]) dfsans1(a+1,b+1);
if(Map[a-1][b-1]&&!vis[a-1][b-1]) dfsans1(a-1,b-1);
}
int temp;
struct data{
int f,s,ds;
}a[100001];
int fa[1001];
bool cmp(data a,data b){
return a.ds<b.ds;
}
int ins(int x,int y,int x1,int y1,int dis){
if(!Map[x1][y1]) return 1;
if(vis[x][y]==vis[x1][y1]) return 0;
temp++;
a[temp].f=vis[x][y];
a[temp].s=vis[x1][y1];
a[temp].ds=dis-1;
return 1;
}
void init(){
for(int i=1;i<=cnt;i++) fa[i]=i;
}
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
void GA(){
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
if(Map[i][j]){
for(int k=i+1;k<=N;k++)
if(!ins(i,j,k,j,k-i)||!ins(i,j,k,j+1,k-i)||!ins(i,j,k,j-1,k-i)) break;
for(int k=i-1;k>=1;k--)
if(!ins(i,j,k,j,i-k)||!ins(i,j,k,j+1,i-k)||!ins(i,j,k,j-1,i-k)) break;
for(int l=j+1;l<=M;l++)
if(!ins(i,j,i,l,l-j)||!ins(i,j,i+1,l,l-j)||!ins(i,j,i-1,l,l-j)) break;
for(int l=j-1;l>=1;l--)
if(!ins(i,j,i,l,j-l)||!ins(i,j,i+1,l,j-l)||!ins(i,j,i-1,l,j-l)) break;
}
}
}
sort(a+1,a+1+temp,cmp);
int ans=0,tmp=0;
init();
for(int i=1;i<=temp;i++){
int xx=find(a[i].f),yy=find(a[i].s);
if(xx!=yy){tmp++;fa[yy]=xx;ans+=a[i].ds;}
}
printf("%d %d\n",tmp,ans);
}
int main(){
N=read(),M=read();
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
cin>>c;
if(c==‘#‘)Map[i][j]=1;
}
}
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
if(!vis[i][j]&&Map[i][j]) dfsans1(i,j),cnt++;
}
}
printf("%d\n",cnt);
if(cnt==0){
printf("0 0\n");
return 0;
}
GA();
return 0;
}
原文:http://www.cnblogs.com/wxjor/p/6964260.html