已知N个正整数：A1、A2、……、An 。今要将它们分成M组，使得各组数据的数值和最平均，即各组的均方差最小。均方差公式如下：
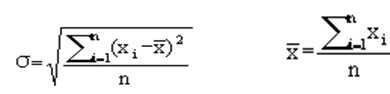
,其中σ为均方差，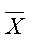
是各组数据和的平均值，xi为第i组数据的数值和。
已知N个正整数：A1、A2、……、An 。今要将它们分成M组，使得各组数据的数值和最平均，即各组的均方差最小。均方差公式如下：
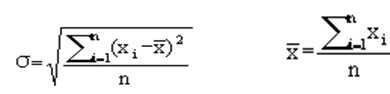
,其中σ为均方差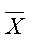，是各组数据和的平均值，xi为第i组数据的数值和。
这一行只包含一个数，表示最小均方差的值(保留小数点后两位数字)。
对于全部的数据，保证有K<=N <= 20，2<=K<=6
AC+1
模拟退火，随机选点更换分组
当温度太大不稳定，直接尝试换到sum最小的组
由于模拟退火的不稳定，所以跑个几万遍就稳了233
当然如果您是yzh那样的强者，您可以用DP每次算最优解
个人认为这样并不优秀，如果您有心情$n ^ 2 m$DP，为何不多退$n ^ 2 m$次火<_<
#include<bits/stdc++.h>
using namespace std;
template <class _T> inline void read(_T &_x) {
int _t; bool flag = false;
while ((_t = getchar()) != ‘-‘ && (_t < ‘0‘ || _t > ‘9‘)) ;
if (_t == ‘-‘) _t = getchar(), flag = true; _x = _t - ‘0‘;
while ((_t = getchar()) >= ‘0‘ && _t <= ‘9‘) _x = _x * 10 + _t - ‘0‘;
if (flag) _x = -_x;
}
using namespace std;
const int maxn = 30;
int n, m, a[maxn];
double ave;
int from[maxn], sum[maxn];
inline double sqr(double val) {return val * val; }
inline double getr() {return (double)rand() / RAND_MAX; }
inline double solve() {
memset(sum, 0, sizeof sum);
for (int i = 1; i <= n; ++i) {
from[i] = rand() % m + 1;
sum[from[i]] += a[i];
}
double ans = 0;
for (int i = 1; i <= m; ++i)
ans += sqr(sum[i] - ave);
double T = 10000;
while (T > 0.1) {
int t = rand() % n + 1, x = from[t], y;
if (T > 1000) y = min_element(sum + 1, sum + m + 1) - sum;
else y = rand() % m + 1;
double to = ans;
to -= sqr(sum[x] - ave) + sqr(sum[y] - ave);
to += sqr(sum[x] - a[t] - ave) + sqr(sum[y] + a[t] - ave);
if (to < ans || exp((ans - to) * 1e4 / T) > getr()) {
ans = to;
from[t] = y;
sum[x] -= a[t], sum[y] += a[t];
}
T *= 0.9;
}
return ans;
}
int main() {
//freopen();
//freopen();
srand(19260817);
read(n), read(m);
for (int i = 1; i <= n; ++i) {
read(a[i]);
ave += a[i];
}
ave /= m;
double ans = solve();
for (int i = 1; i <= 10000; ++i)
ans = min(ans, solve());
printf("%.2lf\n", sqrt(ans / m));
return 0;
}
原文：http://www.cnblogs.com/akhpl/p/6905366.html