这篇文章中包含了对一部分排序的实现,以及常见排序算法性能的比较。
1. 折半插入排序(Binary Insert Sort)实现
2. 插入排序的链表实现
(1) 改变结点值,不改变结点指针
(2) 改变结点指针,不改变结点值
(3) 上面(2) 的简洁版
1. 归并排序实现
2. 归并排序的优化,归并部分不需要判断是否到达末尾。
3. 归并排序的基于链表实现
当我们需要对链表进行排序时,由于不能对它的元素进行随机访问,所以更适合使用归并排序
1. 快速排序实现
2. 快速排序在pivot选择上的优化,从而让划分的子序列长度尽量相等。
1. 堆排序实现
代码:
/** * copyright: Felix Fang @ cnblogs */ #include <stdio.h> //定义链表和相关函数以做备用 struct ListNode{ int m_value; ListNode *m_next; }; ListNode* CreateListNode(int value) { ListNode* pNode = new ListNode(); pNode->m_value = value; pNode->m_next = NULL; return pNode; } void ConnectListNodes(ListNode* pCurrent, ListNode* pNext) { if(pCurrent == NULL) { printf("Error to connect two nodes.\n"); return; } pCurrent->m_next = pNext; } void PrintList(ListNode* pHead) { printf("PrintList starts.\n"); ListNode* pNode = pHead; while(pNode != NULL) { printf("%d\t", pNode->m_value); pNode = pNode->m_next; } printf("\nPrintList ends.\n"); } /** Binary Insert sort 在搜索插入位置使用二分搜索法减小时间复杂度 */ template<typename T> void BinaryInsertSortIncrease(T* list, int size){ if(NULL == list) return; for(int i = 1;i < size;i++){ T temp = list[i]; int start = 0; int end = i-1; //开始遍历0到i-1 while(start < end){ int mid = (start + end)/2; if(temp < list[mid]) end = mid; //end 必须赋值为mid 而不是mid - 1,考虑sart = 0, end = 1的情况,此时进入这行代码,若end = mid-1,则end = -1,后面给temp腾位置时,会把list[-1] 付给 list[0] else if(temp > list[mid]) start = mid + 1; else{ end = mid; break; } } if(list[end] < temp) end++; //不是以beak退出循环时,start == end,这时候再和temp比较一次 for(int k = i; k > end; k--){ list[k] = list[k-1]; } list[end] = temp; } } /** Insert sort based on linked list, change the data of node */ void InsertSortLinkedListIncrease(ListNode *head){ if(NULL == head) return; ListNode *temp = head -> m_next; //从第二个节点开始处理 while(temp != NULL){ ListNode *p = head; while(p -> m_value < temp -> m_value && p != temp){ p = p -> m_next; //在前面已排好序的结点中寻找插入位置 } int moveTempValue = p -> m_value; //开始腾地方,因为是单向链表,只能从前往后遍历,腾地方的时候需要定义一个缓存结点值 p -> m_value = temp -> m_value; while(p != temp){ int tempvalue = p -> m_next -> m_value; p -> m_next -> m_value = moveTempValue; //把缓存结点值(里面存的是p结点原本的值)赋值到 p -> m_next -> m_value moveTempValue = tempvalue; //把 p -> m_next -> m_value原本的值 放到缓存结点。 p = p -> m_next; } temp = temp -> m_next; //处理下一个结点 } } /** Insert sort based on linked list, change the link of nodes rather than data Idea: Divide the orginal linked list into two list, the first one is sorted, second is rest part. Everytime we take the first node from the second list, then find a proper place in first list to insert it. When the second list becomes empty, the first list is the sorted list. */ ListNode * InsertSortLinkedListIncrease_link(ListNode *head){ //注意这次因为链表头结点会更改,因此不能为void类型 if(NULL == head) return NULL; ListNode* head1 = head; ListNode *pre = head; ListNode* temp2 = head1 -> m_next; ListNode* toMove = NULL; head1 -> m_next = NULL; ListNode *temp1 = NULL; while(temp2 != NULL){ if(pre -> m_value > temp2 -> m_value){ //考虑需要插到pre前的情况 head1 = temp2; head1 -> m_next = pre; temp2 = temp2 -> m_next; }else{ while(temp1 != NULL && temp1 -> m_value < temp2 -> m_value){ temp1 = temp1 -> m_next; //pre和temp1两个指针同步移动 pre = pre -> m_next; } toMove = temp2; temp2 = temp2 -> m_next; //第二个链表继续往下遍历 pre -> m_next = toMove; //将这个节点放到第一个链表中,pre和temp1之间 toMove -> m_next = temp1; } pre = head1; temp1 = pre -> m_next; } return head1; } //更加简洁的写法,用for代替了内层while ListNode * InsertSortLinkedListIncrease_linkMoreBrief(ListNode *head){ if(NULL == head) return NULL; ListNode* head1 = head; ListNode *pre = head; ListNode* temp2 = head1 -> m_next; ListNode* toMove = NULL; head1 -> m_next = NULL; ListNode *temp1 = NULL; while(temp2 != NULL){ for(temp1 = head1; temp1 != NULL && temp1 -> m_value < temp2 -> m_value; pre = temp1, temp1 = temp1 -> m_next); if(temp1 == head1){ head1 = temp2; temp2 = temp2 -> m_next; head1 -> m_next = temp1; }else{ toMove = temp2; temp2 = temp2 -> m_next; pre -> m_next = toMove; toMove -> m_next = temp1; } } return head1; } /** Merge sort 归并排序的最好最坏时间复杂度都是O(nlogn),而且稳定 */ template <typename T>void MergeSortCore(T *list1, T *list2, int start, int end); template <typename T>void MergeSortCoreImprove(T *list1, T *list2, int start, int end); template <typename T>void MergeSort(T *list1, int size){ T *list2 = new T[size]; MergeSortCoreImprove(list1, list2, 0, size); } template <typename T>void MergeSortCore(T *list1, T *list2, int start, int end){ if(NULL == list1) return; if(end - start == 1) return; //这一句不可省略,否则 mid==start,进入无限循环 int mid = (start + end)/2; MergeSortCore(list1, list2, start, mid); MergeSortCore(list1, list2, mid, end); //划分子序列,star 到 mid,mid到end分别为两个子序列 for(int i = start;i < end;i++){ list2[i] = list1[i]; //将结果放到list2中,list2作为缓存区,暂存两个子序列内的值。 } int j = start, k = mid, ite = start; while(j < mid && k < end){ if(list2[j] < list2[k]){ list1[ite++] = list2[j++]; }else{ list1[ite++] = list2[k++]; } } while(j < mid) list1[ite++] = list2[j++]; while(k < end) list1[ite++] = list2[k++]; } /** Merge sort improvement 改进版本的归并排序,这个方法可以省去归并最后两步:检测两个子序列中是否有一个还未遍历到末尾。从而提高一些效率。 方法由R.Sedgewick提出 改进的方法是,从list1向 list2复制时,第二个子序列是反向复制的,归并时,第二个子序列也是从末尾遍历到最前进行遍历。 当子序列A到达其末尾时,会因为++再进一位,从而进入另一个子序列B的末尾,这时候它就比B中还未遍历的值都大,所以再往下就会把B中剩余的值复制进去。 */ template <typename T>void MergeSortCoreImprove(T *list1, T *list2, int start, int end){ if(NULL == list1) return; if(end - start == 1) return; int mid = (start + end)/2; MergeSortCoreImprove(list1, list2, start, mid); MergeSortCoreImprove(list1, list2, mid, end); //从开始到这部分都和 MergeSortCore一样 int i = 0; for(i = start; i < mid; i++) list2[i] = list1[i]; for(i = mid; i < end; i++) list2[i] = list1[end + mid - i - 1]; //序列list2反向复制 int j = start, k = end - 1, ite = start; while(ite < end){ if(list2[j] < list2[k]){ list1[ite++] = list2[j++]; }else{ list1[ite++] = list2[k--]; //从两边往中间比较 } } } /** Merge sort based on linked list */ //用于把链表划分为基本相等的两段。遇到空链表或者单节点链表直接返回。 //划分办法为定义两个指针,一个步长1,一个步长2。 ListNode * DivideLinkedList(ListNode *head){ if(head == NULL || head -> m_next == NULL){ return NULL; } ListNode *tempHead = new ListNode(); tempHead -> m_next = head; //定义虚头结点,步长1的指针从这里出发,这样才能保证对于结点数为2的链表,步长1的指针最终落在第一个结点上。 ListNode *step1 = tempHead; ListNode *step2 = head; for(; step2 != NULL; step1 = step1 -> m_next){ step2 = step2 -> m_next; if(step2 != NULL) step2 = step2 -> m_next; } ListNode *temp = step1; temp = temp -> m_next; step1 -> m_next = NULL; return temp; } //这里的Merge采用的是将List2 merge到 List1里的方式,方法有点像前面的InsertSortLinkedListIncrease_linkMoreBrief, //不同的是,这里temp1不需要每次for都要赋初始值。要注意的是:如果list2开始的值都比list1小而且递减(比如 list1: 2,3; list2: -1, -2),merge到list1中时,每次都是加到头结点之前。 //这样就需要修改头结点,temp1也要赋值为新的头结点。 ListNode* MergeLinkedList(ListNode* head1, ListNode* head2){ ListNode* pre = NULL; ListNode* temp1 = head1; ListNode* temp2 = head2; ListNode* newHead = head1; while(temp2 != NULL){ for(; temp1 != NULL && temp1 -> m_value < temp2 -> m_value; pre = temp1, temp1 = temp1 -> m_next); ListNode *toMove = temp2; temp2 = temp2 -> m_next; if(temp1 == newHead){ toMove -> m_next = newHead; newHead = toMove; temp1 = newHead; //调试查出错误后加上,因为头结点被取代了,所以temp1必须手动赋值为新的头结点。 }else{ pre -> m_next = toMove; toMove -> m_next = temp1; } } return newHead; } ListNode* MergeSortLinkedListIncrease(ListNode* head){ if(NULL == head) return NULL; if(head -> m_next == NULL) return head; ListNode* secHead = DivideLinkedList(head); ListNode* firstHead = MergeSortLinkedListIncrease(head); secHead = MergeSortLinkedListIncrease(secHead); return MergeLinkedList(firstHead, secHead); } /** Quick sort 就平均计算时间而言,快速排序是常见内排序算法中最好的。 但在最坏情况(序列已经由小到大排好序),快速排序的递归会成为单支树,每次划分只得到比上次少一个元素的序列。 速度也是O(n^2),而且还慢于插入排序(人家插入排序还能用二分法定位加快速度呢)。 如何才能改进呢? 快排序之所以在对于已经基本有序的序列效率低,是因为我们在实现算法时,取得pivot值是最左边的点(取最右边的也一样),这样pivot基本就是这个序列中最大或者最小值。 导致以这个pivot为基准时,划分出来的两个子序列长度严重不均等。只有当两个子序列基本长度均等,排序的时间才会以log2递减。 那么如何取一个较为合适的pivot呢? 我们本来是将start的值作为中间值,现在我们取 start, end, middle三个地方的值的中位数,把它和left交换下,然后继续把left当作pivot。 */ template <typename T> void QuickSortIncreaseCore(T* list, int start, int end); template <typename T> void QuickSortIncreaseCoreImprove(T* list, int start, int end); template <typename T> void InnerChange(T* list, int left, int right){ T temp = list[left]; list[left] = list[right]; list[right] = temp; } template <typename T> void QuickSortIncrease(T* list, int size){ QuickSortIncreaseCoreImprove(list, 0, size - 1); } template <typename T> void QuickSortIncreaseCore(T* list, int start, int end){ if(NULL == list) return; if(start >= end) return; T pivot = list[start]; int i = start, j = end + 1; do{ do i++; while(list[i] < pivot && i <= end); do j--; while(list[j] > pivot && j >= start); if(i < j) InnerChange(list, i, j); }while(i < j); InnerChange(list, start, j); //此处只能用j不能用i, 考虑{1, 2},此时pivot=1,如果用i, 会导致调用Innerchange(list, 0, 1),结果成了{2, 1} QuickSortIncreaseCore(list, start, j-1); QuickSortIncreaseCore(list, j+1, end); } /** Quick sort improvement */ //获取start, end, middle 三个值的中位数所在的位置 template <typename T> int GetMidianPlace(T* list, int start, int end){ int mid = (start + end)/2; int MedianPlace = 0; T tempSmallValue = list[start] < list[mid] ? list[start] : list[mid]; int tempSmallPlace= list[start] < list[mid] ? start : mid; MedianPlace = tempSmallValue > list[end] ? tempSmallPlace : -1; if(MedianPlace < 0){ tempSmallPlace = tempSmallPlace == mid ? start : mid; MedianPlace = list[end] < list[tempSmallPlace] ? end : tempSmallPlace; } return MedianPlace; } template <typename T> void QuickSortIncreaseCoreImprove(T* list, int start, int end){ if(NULL == list) return; if(start >= end) return; int midianPlace = GetMidianPlace(list, start, end); InnerChange(list, midianPlace, start); T pivot = list[start]; int i = start, j = end + 1; do{ do i++; while(list[i] < pivot && i <= end); do j--; while(list[j] > pivot && j >= start); if(i < j) InnerChange(list, i, j); }while(i < j); InnerChange(list, start, j); //此处只能用j不能用i, 考虑{1, 2},此时pivot=1,如果用i, 会导致调用Innerchange(list, 0, 1),结果成了{2, 1} QuickSortIncreaseCore(list, start, j-1); QuickSortIncreaseCore(list, j+1, end); } /** Heap Sort 堆排序最大的优点在于:一、最坏情况和最好情况下时间复杂度均为 O(nlogn),二、使用的额外空间为O(1),所有的调整都是在list内部 缺点是不能应用在链表上,因为需要大量的非连续访问。 */ //Ajust函数,当左右子树都为最大堆时,adjust可以将root, 左右子树组成的新树调整为最大堆。 template <typename T>void adjust(T* list, int root, int size){ int j = root; while((j * 2 + 1 )< size){ int tempRoot = j; j = j * 2 + 1; if(j+1 < size && list[j+1] > list[j]) j++; if(list[j] > list[tempRoot]){ InnerChange(list, j, tempRoot); }else{ break; } } } template <typename T>void HeapSortIncrease(T* list, int size){ if(NULL == list) return; if(size <= 1) return; for(int i = (size - 2)/2; i >= 0;i--)//这部分for的时间复杂度为O(n/2logn) adjust(list, i, size); //先将现有的数组调整成一个最大堆,从号码最大的非叶节点开始,逐次往前调用adjust 即可。 for(int j = size-1;j > 0;j--){ InnerChange(list, j, 0); //每次将最大堆的根结点提出,和最末的结点交换位置。 adjust(list, 0, j); //将除最末结点外的部分adjust成新的最大堆。这部分for的时间复杂度为O(nlogn) } } int main(){ int i = 0; //测试二分插入排序 /*int test[10] = {3, 6, 5, 2, 6, 12, 16, 9, 7, 8}; int test2[5] = {100, 90, 70, 60, 50}; int test3[1] = {1}; BinaryInsertSortIncrease(test, 10); for(i = 0;i < 10;i++){ printf("%d ", test[i]); } printf("\n"); BinaryInsertSortIncrease(test2, 5); for(i = 0;i < 5;i++){ printf("%d ", test2[i]); } printf("\n"); BinaryInsertSortIncrease(test3, 1); for(i = 0;i < 1;i++){ printf("%d ", test3[i]); } printf("\n");*/ //测试基于链表的插入排序,改变结点值 /*ListNode* pNode1 = CreateListNode(1); ListNode* pNode2 = CreateListNode(6); ListNode* pNode3 = CreateListNode(5); ListNode* pNode4 = CreateListNode(2); ListNode* pNode5 = CreateListNode(8); ConnectListNodes(pNode1, pNode2); ConnectListNodes(pNode2, pNode3); ConnectListNodes(pNode3, pNode4); ConnectListNodes(pNode4, pNode5); PrintList(pNode1); InsertSortLinkedListIncrease_link(pNode1); PrintList(pNode1); InsertSortLinkedListIncrease_link(NULL); ListNode* pNode21 = CreateListNode(5); InsertSortLinkedListIncrease_link(pNode21); PrintList(pNode21);*/ //测试基于链表的插入排序,改变结点指针 /*ListNode* lNode1 = CreateListNode(2); ListNode* lNode2 = CreateListNode(5); ListNode* lNode3 = CreateListNode(7); ListNode* lNode4 = CreateListNode(3); ListNode* lNode5 = CreateListNode(2); ConnectListNodes(lNode1, lNode2); ConnectListNodes(lNode2, lNode3); ConnectListNodes(lNode3, lNode4); ConnectListNodes(lNode4, lNode5); PrintList(lNode1); lNode1 = InsertSortLinkedListIncrease_link(lNode1); PrintList(lNode1); InsertSortLinkedListIncrease_link(NULL); ListNode* lNode21 = CreateListNode(5); lNode21 = InsertSortLinkedListIncrease_link(lNode21); PrintList(lNode21);*/ //测归并排序 /*int test31[10] = {3, 6, 5, 2, 6, 12, 16, 9, 7, 8}; int test32[5] = {90, 100, 70, 60, 50}; int test33[1] = {1}; MergeSort(test31, 10); for(i = 0;i < 10;i++){ printf("%d ", test31[i]); } printf("\n"); MergeSort(test32, 5); for(i = 0;i < 5;i++){ printf("%d ", test32[i]); } printf("\n"); MergeSort(test33, 1); for(i = 0;i < 1;i++){ printf("%d ", test33[i]); } printf("\n");*/ //测试基于链表的归并排序 /*ListNode* lNode41 = CreateListNode(2); ListNode* lNode42 = CreateListNode(3); ListNode* lNode43 = CreateListNode(1); ListNode* lNode44 = CreateListNode(-1); ListNode* lNode45 = CreateListNode(-2); ConnectListNodes(lNode41, lNode42); ConnectListNodes(lNode42, lNode43); ConnectListNodes(lNode43, lNode44); ConnectListNodes(lNode44, lNode45); PrintList(lNode41); lNode41 = MergeSortLinkedListIncrease(lNode41); PrintList(lNode41); MergeSortLinkedListIncrease(NULL); ListNode* lNode431 = CreateListNode(5); lNode431 = MergeSortLinkedListIncrease(lNode431); PrintList(lNode431);*/ //测试快速排序 /*int test5[10] = {3, 6, 5, 2, 6, 12, 16, 9, 7, 2}; int test52[5] = {100, 90, 70, 60, 50}; int test53[1] = {1}; QuickSortIncrease(test5, 10); for(i = 0;i < 10;i++){ printf("%d ", test5[i]); } printf("\n"); QuickSortIncrease(test52, 5); for(i = 0;i < 5;i++){ printf("%d ", test52[i]); } printf("\n"); QuickSortIncrease(test53, 1); for(i = 0;i < 1;i++){ printf("%d ", test53[i]); } printf("\n");*/ //测试堆排序 int test6[10] = {3, 6, 5, 2, 6, 12, 16, 9, 7, 2}; int test62[5] = {100, 50, 70, 60, 50}; int test63[1] = {1}; HeapSortIncrease(test6, 10); for(i = 0;i < 10;i++){ printf("%d ", test6[i]); } printf("\n"); HeapSortIncrease(test62, 5); for(i = 0;i < 5;i++){ printf("%d ", test62[i]); } printf("\n"); HeapSortIncrease(test63, 1); for(i = 0;i < 1;i++){ printf("%d ", test63[i]); } printf("\n"); }
稳定性是指值相等的结点在排序后相对位置没有被打乱。A==B,在原序列中A在B前,排序后A依然在B前面。
稳定排序算法的优势:可以基于不同的key对序列进行多次排序。比如数据库中可以基于多个列作Index,假设列A和列B,先基于列A作排序,排序完后再基于列B做排序。如果第二次排序时我们选择的算法是稳定的,我们就可以使数据按照B列上的顺序排列,对于B列上的值相等的数据,他们仍会按照A列上的值顺序排列。在数据库中查找数据时,基于这两个列的Index就发挥作用了。
具体关于排序算法性能的比较,参见下图:
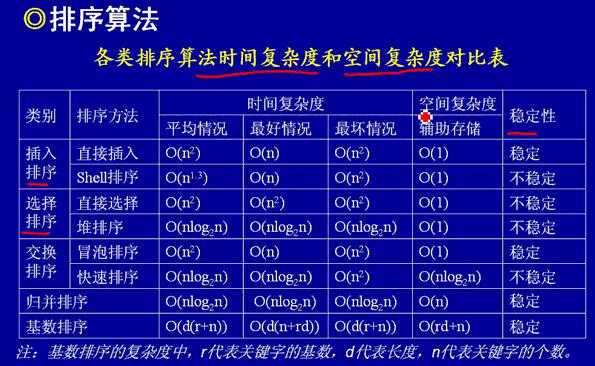
图片来自 http://blog.csdn.net/winniepu/article/details/3928363
本文代码部分为原创,部分优化思路参考自《数据结构》第二版,殷人昆主编,清华大学出版社,第9章 排序。
常见内排序实现汇总(含部分优化实现,基于链表的实现),以及性能比较
原文:http://www.cnblogs.com/felixfang/p/3537503.html