★★☆ 输入文件：flowa.in 输出文件：flowa.out 简单对比
时间限制：1 s 内存限制：128 MB
【问题描述】
Bob 觉得一般图的最大流问题太难了，他不知道如何解决，于是他想尝试一个简单点的：栅格网络中的最大流问题，这个虽说简单了一点，但对 Bob 来说依旧太难，现在他有个麻烦需要你帮忙：给你一个 N*M 的栅格（如下所示），栅格中的边表示可以流水的管道，边上的数字表示管道的容量，举例说明：在下面图（ 2.6.1 ）中， (0,0) 和 (1,0) 之间边的容量为 6 ，这意味着这条边（水管）的最大水流量不超过 6 个单位。
N=3 M=3
图 2.6.1 栅格网络流
那么栅格中从 S 到 T 的最大流是多少呢 ? 换句话说 , 某一时刻最多能有多少单位的水从 S 流向 T?
【输入格式】
输入文件的第一行是一个正整数 T ，表示接下来有多少组测试数据。
每一组测试数据的第一行有两个正整数 N,M(1<=N,M<=100)<n<100) 和="" m(1<m<100)="" 。接下来有两个整数矩阵="" h="" （="" n*(m-1)="" ）和="" v="" (n-1)*m="" ），="" h[i][j]="" 表示="" (i,j)="" 与="" (i,j+1)="" 之间边的容量，="" v[i][j]="" (i+1,j)="" 中所有的数均非负且小于="" 10^10="" 。<="" p="">
接着有两个矩阵H(N*(M-1)),V((N-1)*M)，H[i][j]表示(i,j)->(i,j+1)的流量；
V[i][j]表示(i,j)->(i+1,j)的流量。
【输出格式】
每一组测试数据输出只有一行，包含一个整数，即从 S(0,0) 到 T(N-1,M-1) 的栅格网络的最大流，不允许出现多余的空格。
【输入样例】
输入文件名： flowa .in
1
3 3
0 1
2 3
4 5
6 7 8
9 10 11
输出文件名： flowa .out
6
提示：下图 (2.6.2) 所示即为样例中栅格中的一个最大流。
N=3 M=3
图 2.6.2 一个解决方案
思路：对偶图转化+SPFA
这个图直接跑最大流会T的（师傅说的）。
先把图重构，然后跑一个最小截断路（最小割）。
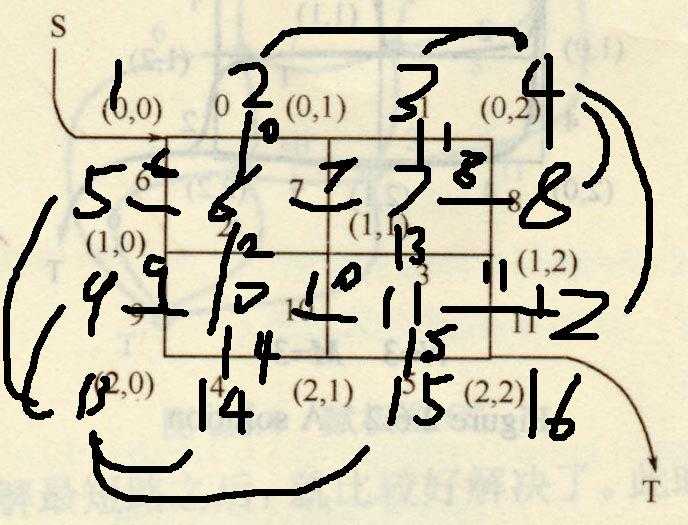构图，like this.
代码实现：
1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #define inf 1000000000000000ll 5 using namespace std; 6 int test,n,m,s,t; 7 int a,b,c,l; 8 int h[12100],hs=1; 9 struct edge{int s,n;long long w;}e[300000]; 10 int q[300000],head,tail; 11 long long la,lb; 12 long long w[12100]; 13 char ch[30]; 14 long long read(){ 15 long long ret=0;l=0; 16 do{ch[0]=getchar();}while(ch[0]<‘0‘||ch[0]>‘9‘); 17 l++; 18 do{ch[l++]=getchar();}while(ch[l-1]>=‘0‘&&ch[l-1]<=‘9‘); 19 l-=2; 20 for(long long i=l,j=1;i>=0;i--,j*=10) ret+=(ch[i]-‘0‘)*j; 21 return ret; 22 } 23 void write(long long x){ 24 if(!x) return; 25 write(x/10); 26 putchar(x%10+‘0‘); 27 } 28 int main(){ 29 freopen("flowa.in","r",stdin); 30 freopen("flowa.out","w",stdout); 31 scanf("%d",&test); 32 while(test--){ 33 memset(h,0,sizeof(h)),hs=0; 34 scanf("%d%d",&n,&m); 35 s=m+1,t=n*m+n+1; 36 for(int i=2;i<=m;i++){ 37 a=n*m+n+i; 38 e[++hs]=(edge){i,h[s],0},h[s]=hs; 39 e[++hs]=(edge){t,h[a],0},h[a]=hs; 40 } 41 for(int i=1;i<n;i++){ 42 a=(i+1)*(m+1),b=i*(m+1)+1; 43 e[++hs]=(edge){a,h[s],0},h[s]=hs; 44 e[++hs]=(edge){t,h[b],0},h[b]=hs; 45 } 46 for(int i=1;i<=n;i++) 47 for(int j=1;j<m;j++){ 48 la=read(); 49 b=i*m-m+i+j,c=b+m+1; 50 e[++hs]=(edge){c,h[b],la},h[b]=hs; 51 e[++hs]=(edge){b,h[c],la},h[c]=hs; 52 } 53 for(int i=1;i<n;i++) 54 for(int j=1;j<=m;j++){ 55 la=read(); 56 b=i*m+i+j+1,c=b-1; 57 e[++hs]=(edge){c,h[b],la},h[b]=hs; 58 e[++hs]=(edge){b,h[c],la},h[c]=hs; 59 } 60 for(int i=1;i<=(n+1)*(m+1);i++) w[i]=inf; 61 head=tail=0; 62 w[s]=0,q[head++]=s; 63 while(head>tail){ 64 a=q[tail++]; 65 for(int i=h[a];i;i=e[i].n){ 66 la=w[a]+e[i].w,lb=w[e[i].s]; 67 if(la<lb) w[e[i].s]=la,q[head++]=e[i].s; 68 } 69 } 70 write(w[t]); 71 if(!w[t]) putchar(‘0‘); 72 putchar(‘\n‘); 73 } 74 return 0; 75 }
开long long！！！
题目来源：COGS
原文：http://www.cnblogs.com/J-william/p/6538485.html