如题,给出一个网络图,以及其源点和汇点,每条边已知其最大流量和单位流量费用,求出其网络最大流和在最大流情况下的最小费用。
输入格式:
第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含四个正整数ui、vi、wi、fi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi),单位流量的费用为fi。
输出格式:
一行,包含两个整数,依次为最大流量和在最大流量情况下的最小费用。
4 5 4 3 4 2 30 2 4 3 20 3 2 3 20 1 2 1 30 9 1 3 40 5
50 280
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=10
对于70%的数据:N<=1000,M<=1000
对于100%的数据:N<=5000,M<=50000
样例说明:
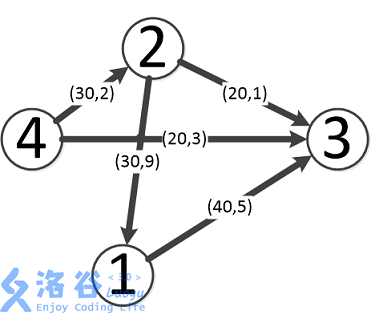
如图,最优方案如下:
第一条流为4-->3,流量为20,费用为3*20=60。
第二条流为4-->2-->3,流量为20,费用为(2+1)*20=60。
第三条流为4-->2-->1-->3,流量为10,费用为(2+9+5)*10=160。
故最大流量为50,在此状况下最小费用为60+60+160=280。
故输出50 280。
思路:费用流
因为要注意费用的问题,所以用SPFA找费用最小的增广路,不要用Dijkstra(因为有负边权);
然后增广。
几个注意的地方:
反边费用为其对应边的相反数;
队列首尾指针记得清零;(RE了50%左右)
有一种优化技巧叫先留个坑,反边随用随建。
代码实现:
1 #include<cstdio> 2 #include<cstring> 3 #define maxn 5010 4 #define maxm 100010 5 #define maxt 2139062143 6 int n,m,s,t,nflow,nfee,flow,fee; 7 int a,b,c,d; 8 long long la,lb; 9 int h[maxn],hs=1; 10 struct edge{int s,n,w,f;}e[maxm]; 11 int w[maxn]; 12 int p[maxn][2]; 13 int q[maxm],head,tail; 14 int min(int x,int y){return x<y?x:y;} 15 int spfa(){ 16 memset(w,0x7f,sizeof(w)); 17 head=tail=0; 18 q[head++]=s,w[s]=0; 19 while(head>tail){ 20 a=q[tail++]; 21 for(int i=h[a];i;i=e[i].n) 22 if(e[i].w){ 23 la=e[i].f,lb=w[a],la+=lb,lb=w[e[i].s]; 24 if(la<lb){ 25 w[e[i].s]=la; 26 p[e[i].s][0]=i; 27 p[e[i].s][1]=a; 28 q[head++]=e[i].s; 29 } 30 } 31 } 32 return w[t]; 33 } 34 int ap(int k,int v){ 35 if(k==s) return v; 36 int ret=ap(p[k][1],min(e[p[k][0]].w,v)); 37 if(!e[p[k][0]^1].f) e[p[k][0]^1]=(edge){p[k][1],h[k],0,-e[p[k][0]].f},h[k]=p[k][0]^1; 38 e[p[k][0]].w-=ret; 39 e[p[k][0]^1].w+=ret; 40 return ret; 41 } 42 bool Dinic(){ 43 nfee=spfa(); 44 if(nfee==maxt) return false; 45 nflow=ap(t,maxt); 46 flow+=nflow; 47 fee+=nflow*nfee; 48 return true; 49 } 50 int main(){ 51 scanf("%d%d%d%d",&n,&m,&s,&t); 52 for(int i=1;i<=m;i++){ 53 scanf("%d%d%d%d",&a,&b,&c,&d); 54 e[++hs]=(edge){b,h[a],c,d},h[a]=hs++; 55 } 56 while(Dinic()); 57 printf("%d %d\n",flow,fee); 58 return 0; 59 }
题目来源:洛谷
原文:http://www.cnblogs.com/J-william/p/6506067.html