[codeforces494B]Obsessive String
试题描述
Hamed has recently found a string t and suddenly became quite fond of it. He spent several days trying to find all occurrences of t in other strings he had. Finally he became tired and started thinking about the following problem. Given a string s how many ways are there to extract k?≥?1 non-overlapping substrings from it such that each of them contains string t as a substring? More formally, you need to calculate the number of ways to choose two sequences a1,?a2,?...,?ak and b1,?b2,?...,?bksatisfying the following requirements:
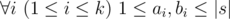
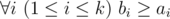
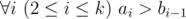
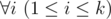t is a substring of string sa_isa_i?+?1... sb_i (string s is considered as 1-indexed).As the number of ways can be rather large print it modulo 109?+?7.
输入
Input consists of two lines containing strings s and t (1?≤?|s|,?|t|?≤?105). Each string consists of lowercase Latin letters.
输出
Print the answer in a single line.
输入示例
welcometoroundtwohundredandeightytwo
d
输出示例
274201
数据规模及约定
见“输入”
题解
首先用 KMP 预处理一波数组 pos[i]，表示串 s 第 i 位左边最靠右的那次对于 t 的完整匹配的左端点（有点拗口，举个栗子 s = "ababa"，那么 pos[i] = {0, 0, 1, 1, 3}）。
有了 pos 数组，就可以 dp 了。我们考虑每个位置放置一个左端点，或是一个右端点，或者不放（注意不放有两种情况，一种是刚放完左端点，一种是刚放完右端点）；于是设 f[i][0] 表示最后一次放的是左端点，放在了位置 i 或者 i 的左边；f[i][1] 表示最后一次放的是右端点，放在了位置 i 或 i 的左边。转移时就是考虑当前这个位置放置还是不放，具体转移方程留给读者思考。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = getchar(); }
return x * f;
}
#define maxn 100010
#define MOD 1000000007
char S[maxn], T[maxn];
int Fail[maxn], pos[maxn], f[maxn][2];
int main() {
scanf("%s%s", S + 1, T + 1);
int n = strlen(S + 1), m = strlen(T + 1);
for(int i = 2; i <= m + 1; i++) {
int j = Fail[i-1];
while(j > 1 && T[j] != T[i-1]) j = Fail[j];
Fail[i] = T[j] == T[i-1] ? j + 1 : 1;
}
int p = 1;
for(int i = 1; i <= n; i++) {
while(p > 1 && T[p] != S[i]) p = Fail[p];
p = T[p] == S[i] ? p + 1 : 1;
if(p == m + 1) pos[i] = i - m + 1;
}
for(int i = 1; i <= n; i++) if(!pos[i]) pos[i] = pos[i-1];
// for(int i = 1; i <= n; i++) printf("%d%c", pos[i], i < n ? ‘ ‘ : ‘\n‘);
f[0][1] = 1;
for(int i = 1; i <= n; i++) {
f[i][0] = (f[i-1][0] + f[i-1][1]) % MOD;
f[i][1] = (f[i-1][1] + (pos[i] ? f[pos[i]][0] : 0)) % MOD;
// printf("(%d, %d)%c", f[i][0], f[i][1], i < n ? ‘ ‘ : ‘\n‘);
}
printf("%d\n", (f[n][1] ? f[n][1] : MOD) - 1);
return 0;
}
[codeforces494B]Obsessive String
原文：http://www.cnblogs.com/xiao-ju-ruo-xjr/p/6480821.html