最近做到一个关于杨氏矩阵的题目。 UVALive 6625
题目大意是用n以内的数填充杨氏矩阵,要求行严格递增,列不严格递增。 求方案数。
数据范围很小,我直接上爆搜,结果TLE了。 后来发现一位学长用爆搜过了,可能和搜索顺序有点关系,我是按列搜索,学长是按行。
此题的标算应该是状压dp,因为按行是严格递增的,所以可以 按列划分阶段,状态存储这一行用了哪些数即可。
其实这题还可以直接套公式。
行和列都严格递增的杨氏矩阵 方案数是 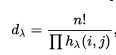
行严格递增列不严格自增的方案数是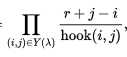
参考下面的文章
https://en.wikipedia.org/wiki/Young_tableau
https://en.wikipedia.org/wiki/Hook_length_formula
对于第一个公式的详细证明 可以看下面这篇论文:
http://ocw.library.nenu.edu.cn/pluginfile.php/30614/mod_resource/content/1/Probabilistic%20proof.pdf
第二个公式的证明 我在网上没能找到...就当是个偏门的小知识记住吧。
Hook length formula 学习笔记 UVALive 6625
原文:http://www.cnblogs.com/vb4896/p/6397139.html