Deep Learning（Bengio）2.1-2.6节 读书笔记 - 线性代数之一

第二章 线性代数

2.1 标量、向量、矩阵和张量
这一章讲述了下面几个基本概念：
1. 标量（scalar），用斜体表示，如a
2. 向量（vector），有序数列，用粗体小写字母表示，如a
3. 矩阵（matrix），二维数组，用粗体大写字母表示，如A
4. 张量（tensor），理解为多维数组吧。
以及一些操作：
1. 转置（transpose），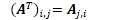

2. 矩阵加法，即相应位置的元素相加
3. 矩阵与标量的加法与乘法，即相应位置的元素与标量相加或相乘
4. 在深度学习中，允许矩阵和向量相加，得到另一个矩阵。操作是向量b和矩阵A的每一行相加。这种隐式地复制向量b到很多位置的方式，被称为广播（broadcasting）。

2.2 矩阵和向量相乘
概念：
1. 矩阵乘积（matrix product），矩阵A左乘矩阵B，要求A的列数必须和B的行数相等。操作是：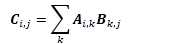

这个公式虽然用得稀疏平常，但我却不清楚他的物理意义，难以在大脑里对它有个形象的理解，权当做为了使这乘法有较好的性质才如此定义。甚至，我连矩阵的物理意义尚且不明了。
2. 元素对应乘积（element-wise product），又称Hadamand乘积（Hadamand product），即两矩阵对应元素乘积，符号为A⊙B
矩阵操作的一些性质：
1. 分配率：A(B+C) = AB+BC
2. 结合律：A(BC) = (AB)C
3. 不满足交换率：AB = BA并非总是满足
4. 

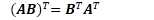
2.3 单位矩阵和逆矩阵
概念：
1. 单位矩阵（indentity matrix），主对角线都是1，其他位置都是0的方阵。任意向量与之相乘不会改变。正方形矩阵亦然。符号为

2. 逆矩阵（martix inverse），符号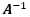为，定义为：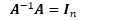

2.4 线性相关和生成子空间
这里我们主要讨论 Ax = b 这个方程。其中A是m×n的矩阵（m行n列），x和b都是m维向量，x是未知数。
我们来分析这个方程有多少个解。
先抛出两个推论：
1. 如果矩阵A的逆矩阵存在，那么对应所有的向量b，x有唯一解。（易证：原式子中等号两边左乘A的逆矩阵即可）
2. 不存在多于一个解且少于无限个解的情况。（易证：假设x和y都是方程的解，那么z=ax+(1-a)y也是方程的解）

再来一个观点（理解方法）：
把A拆成一列一列的，得到一个列向量的集合。然后组合这些向量，允许任意放缩，使之相加，最终得到向量b，那么这个组合就是方程的一组解。每个列向量的放缩系数组成的向量，即x的一个可行取值。
（书上的说法是：我们可以将A的列向量看作是从原点(origin)（元素都是零的向量）出发的不同方向，确定有多少种方法可以到达向量b。在这个观点中，向量x中的每个元素表示我们应该沿着这些方向走多远，即x_i 表示我们需要沿着第i个向量的方向走多远。）
1. 这种操作被称为线性组合（linear combination）。
2. 一组向量的生成子空间（span）是原始向量线性组合后所能达到的点的集合
3. A的列空间（column space）/A的值域（range），即矩阵A的列向量的生成子空间。
4. 线性相关（linear dependence），即某一向量能被其他向量线性组合得到。
5. 线性无关（linearly independent），即一组向量中任一个向量都不能由其他向量线性组合得到。
6. 奇异的（singular），一个列向量线性相关的方阵。

对于所有实数空间内的b，要使方程有唯一解，有两个条件，一是m=n，二是所有列向量线性无关。

书上提到一句：
如果矩阵A不是一个方阵或者是一个奇异的方阵，该方程仍然可能有解。但是我们不能使用逆矩阵去求解。
这是因为，如果它不是一个方阵，则违反了上面的条件一；如果它奇异，则违反了条件二。
又，如果矩阵A有逆矩阵，那么对于所有的b，方程有唯一解（前面的推论1）。
故而这种情况，不能用逆矩阵去求解。

2.5 范数
衡量一个向量的大小的东西。范数的要求是：
1. f(x) = 0 => x = 0
2. f(x + y) ≤ f(x) + f(y) （三角不等式(triangle inequality)）
3.

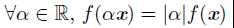
通常使用L^p 范数。定义如下：

通常采用p=1，p=2（欧几里得范数），p=∞（max范数）。不难理解其各自的性质。

矩阵的范数常用Frobenius范数：

跟向量的L² 范数差不多。

2.6 特殊类型的矩阵和向量
这里讲了一些概念:
1. 对角矩阵（diagonal matrix），只有主对角线上含有非零元素，其他位置都是零。可以表示为diag(v)，表示主对角线上元素由向量v构成的对角矩阵。
2. 对称（symmetric）矩阵，转置和自己相等的矩阵。
3. 单位向量（unit vector），具有单位范数（unit norm）的向量。这里单位范数指的是L² 范数为1。
4. 向量正交（orthogonal），当x^Ty=0
5. 标准正交（orthonormal），向量正交，且他们的范数都是1
6. 正交矩阵（orthogonal matrix），指行向量标准正交，列向量标准正交的方阵。

我发现上面写着写着，就像是提取书本大纲一样，其实没什么好提取的，不如直接看书。
接下来改一下姿势，主要是写自己的感悟、总结和自己个人相对较关注的点就好了。不再赘述书本内容。

Deep Learning（Bengio）2.1-2.6节 读书笔记 - 线性代数之一

原文：http://www.cnblogs.com/windeng/p/6373676.html