前面,针对图片训练了简单的逻辑分类器,现在,我们会将该分类器转变为深度网络
只需要几行代码就能搞定,所以一定要确保十分理解之前的内容。
在第二部分,将简单地介绍如何完全通过优化器计算任意函数的斜率
第三部分,将学习一个重要的概念 即规则化,通过规则化我们能够训练更加庞大的模型
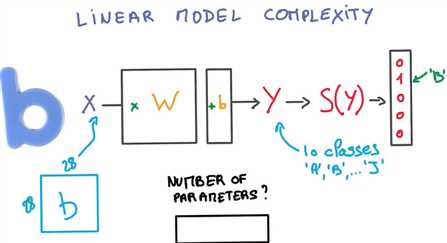
目前训练的简单模型看起来不错,但是功能却有限,不妨思考个问题,该模型世界上有多少个训练参数?
提醒下 每个输入值都是28*28的图片 输出值是10个类
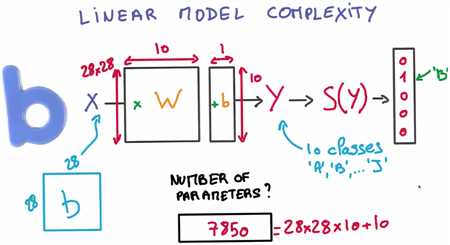
矩阵W 取整个28*28像素的图像作为输入,输出大小是10 所以矩阵的另一个维度是10
偏置向量是1*10,所以参数的总数目是
Total number of parameters
= size of W + size of b
= 28x28x10 + 10
= 7850
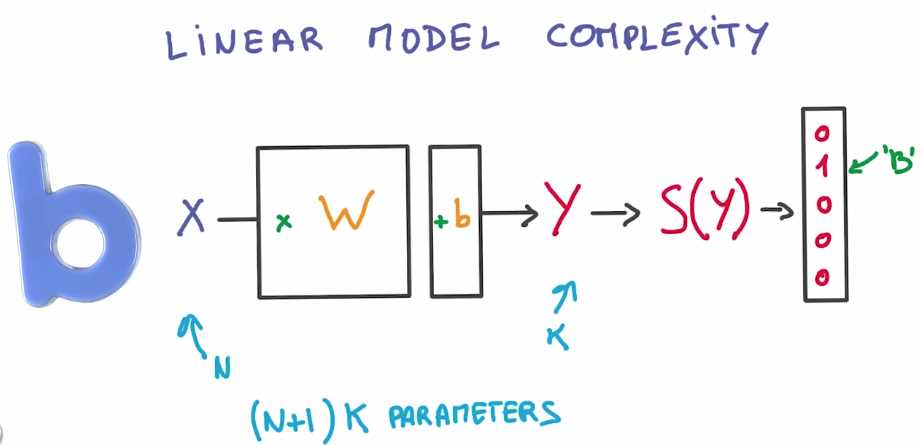
这是一般情况,如果你有N个输入值 K个输出值 则可以使用(N+1)K个参数,不能再多了
问题是 实际上你可能需要使用多得多的参数。
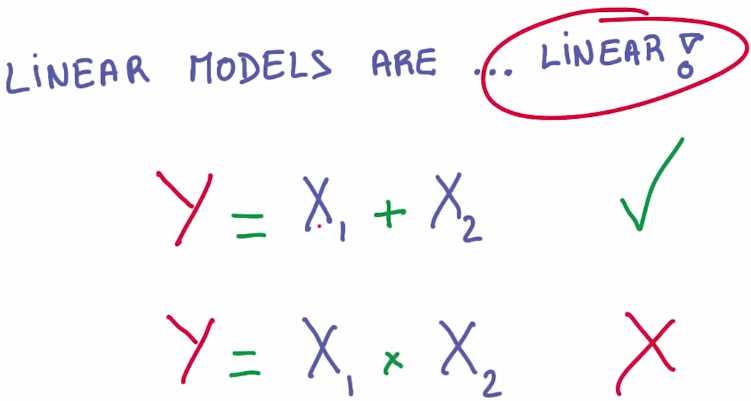
而且该算式是线性的。这意味着你使用该模型,能够表示的算式关系是有限的
例如 如果两个输入值的算式关系是相加,则你的模型可以通过矩阵相乘来很好的表示这一关系
但是 如果两个输入值的算式关系是相乘,则无法使用线性模型有效地表示这一关系
但是线性运算本身还是很有用的,大的矩阵相乘正是图形处理器的设计宗旨
图形处理器相对来说成本低廉而且速度非常快
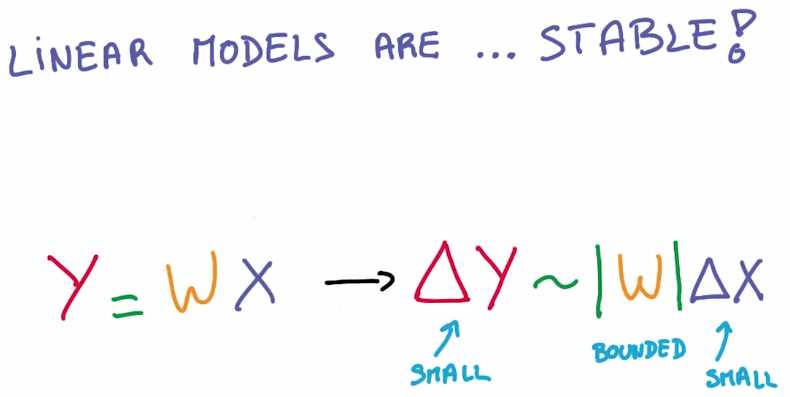
从数学角度来讲 线性运算非常稳定,我们可以通过数学公式来演示,
输入值得小小变化绝对不会使输出值出现非常大的波动
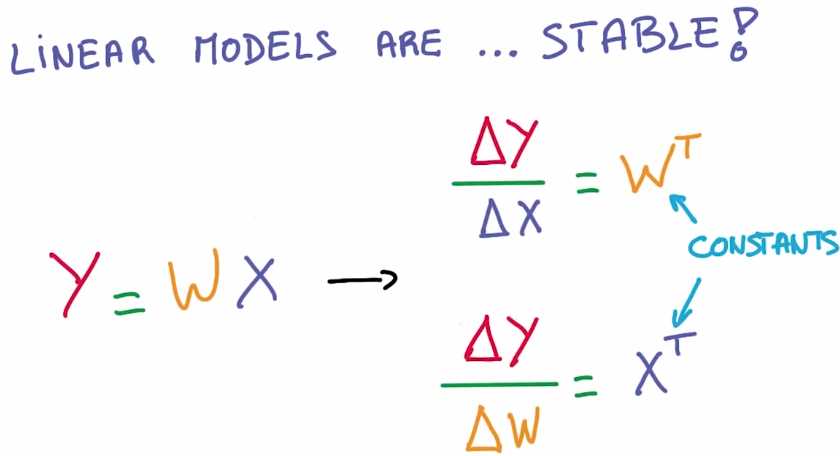
其中的导数也很理想,线性函数的导数是常量,在数学上没有什么比常量更加稳定的了
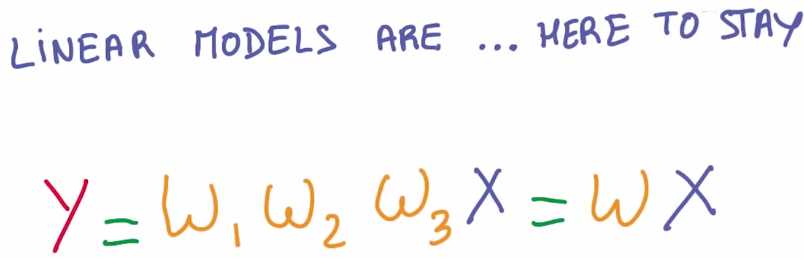
我们希望将参数保持在大的线性函数里面,但是又希望整个模型是非线性的
我们不能仅仅通过线性函数将输入值不断地相乘,因为这就等同于一个大的线性函数
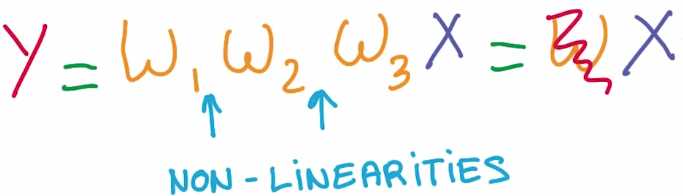
因此现在介绍的是非线性函数
现在介绍偷懒的工程师最喜欢使用的非线性函数 修正线性单元(the rectified linear units)简称ReLU
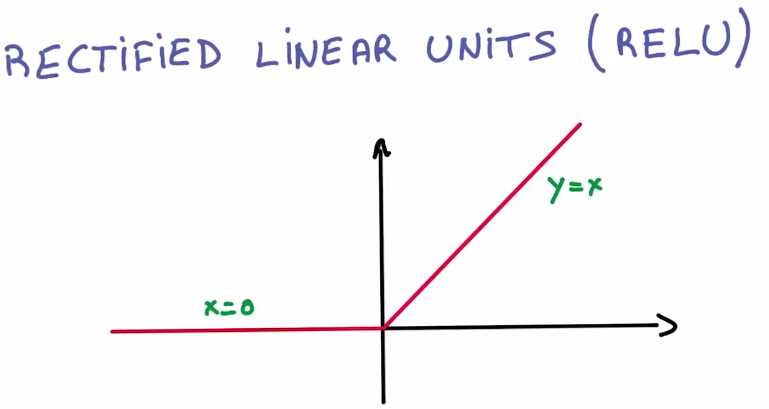
ReLU 绝对是你能够想到的最简单的非线性函数,如果x大于0则是线性函数,如果x小于等于0 输出就保持为0
ReLU 的导数也很理想the derivative of the segment to the left would be zero, as the value remains constant (x=0), and to the right would be a constant (=1) since it grows linearly (y=x).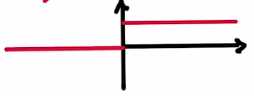
因为我们是偷懒工程师,所以我们需要运用能够派的上用场的工具,
也就是逻辑分类器 只需要稍加修改 就能变成非线性函数
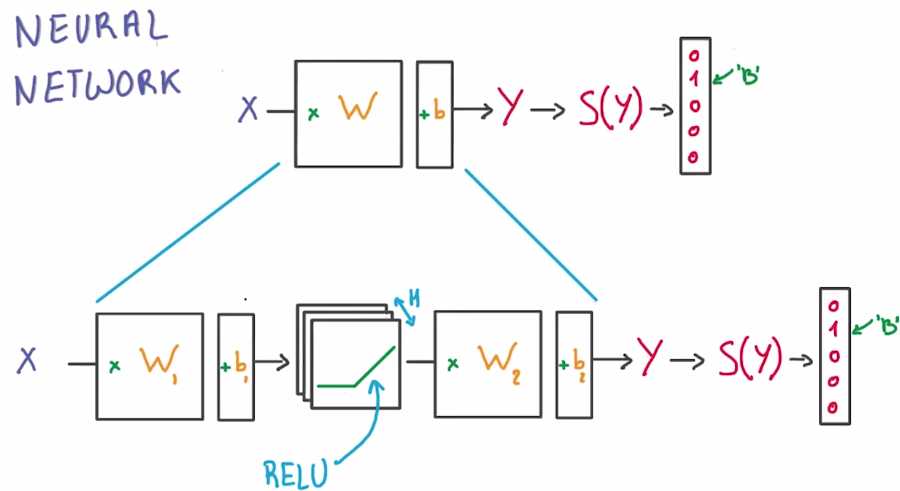
我们将用最简便的方法构建新的函数 我们将直接在公式中间插入一个ReLU
而不是将单个矩阵因子当做分类器。现在我们获得了两个矩阵
一个将输入值传递到ReLU中,一个将ReLU与分类器相连。我们已经解决了两个问题
通过在中间插入ReLU函数现在已经变成非线性函数
我们现在已经找到可以调节公式的新切入点,这里的H对应的是分类器中ReLU的个数
我们可以根据需要将H调的非常大。这就已经构建了第一个神经网络
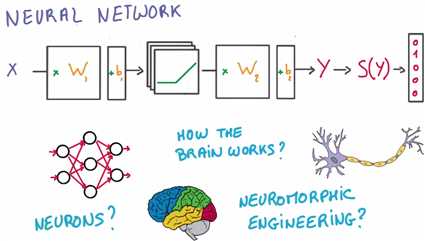
你可能想问,神经元在哪里呀?
过去 提到神经网络 我能记起的都是由树突和轴突组成的图表 还有激发函数、大脑、神经科学,这些都在哪里?
是的,我们可以用神经网络来比喻大脑,这样很直观,甚至可能是正确的,但是其中涉及到的知识太复杂了
而且有时候可能会让你走偏了,所以在本课程中,不会介绍神经网络。
我们不需要成为巫师或科学家,如果你是个偷懒的工程师,拥有一个大的图形处理器
并且只想机器学习的效果能更好,则构建神经网络自然是最合理的选择。
但是,我们需要好好地讲讲数学原理了
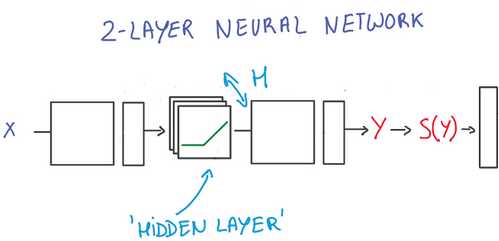
注意:以上描述的是一个“两层”神经网络
1、第一层是由一组X的权重和偏差组成并通过ReLU函数激活。
这一层的输出会提供给下一层,但是在神经网络的外部不可见,一次被称为隐藏层
2、第二层有隐藏层的权重和偏差组成,隐藏层的输入即为第一层的输出,然后由
Softmax函数来生成概率
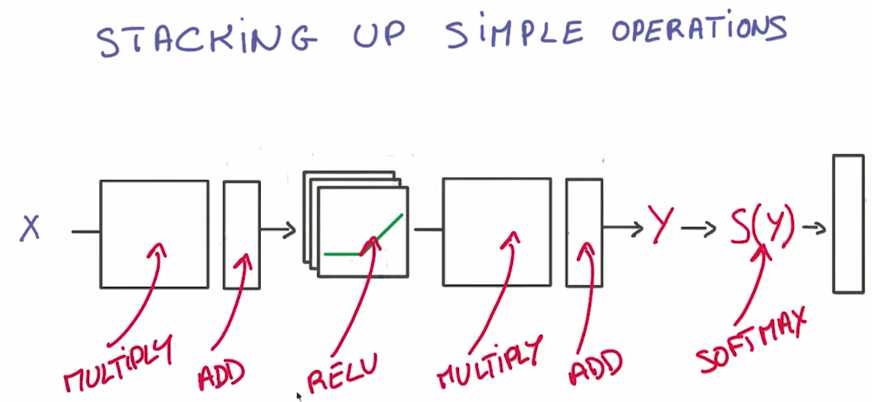
为何要通过将简单的运算公式,例如相乘,相加还有ReLU,相互叠加在一起构建一个网络
原因很简单,因为这在数学上是非常简单的,简单到深度学习框架能够帮你实现
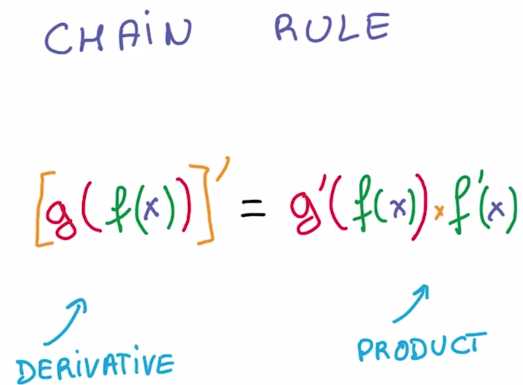
关键的数学点是链式法则(chain rule)
如果你有两个组合函数,将一个函数的结果运用到另一个函数中,则利用链式法则
你可以求出这个组合函数的导数,只需要求出各部分的导数并计算他们的乘积
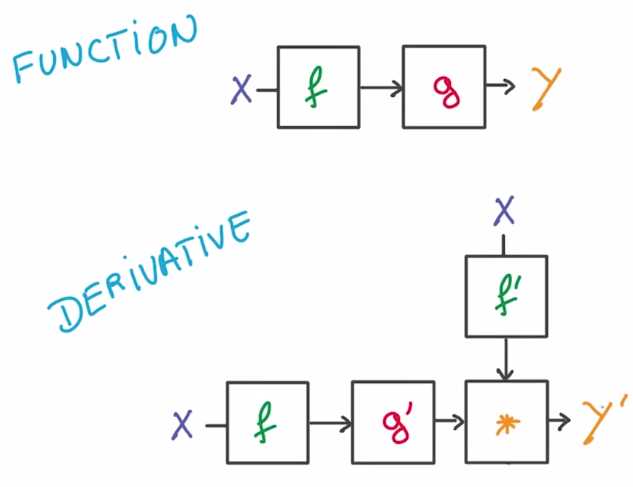
作用太强大了,只要你知道如何写出大哥函数的导数,就有一个简单的图形方法将他们结合到一起
并计算出整个函数的导数。从计算机科学家角度来说,这更是个好消息了

有一个编写该链式法则的非常高效的计算方法,你可以多次重复使用数据
看起来就像个简单的数据管道

假设你的神经网络 是由一系列的简单运算构成,譬如线性变换、ReLU等等
有的变换有参数,如矩阵变换,有的则没有,如ReLU
当你把数据输入到x,它们将会经过这堆运算,然后得到预测值y
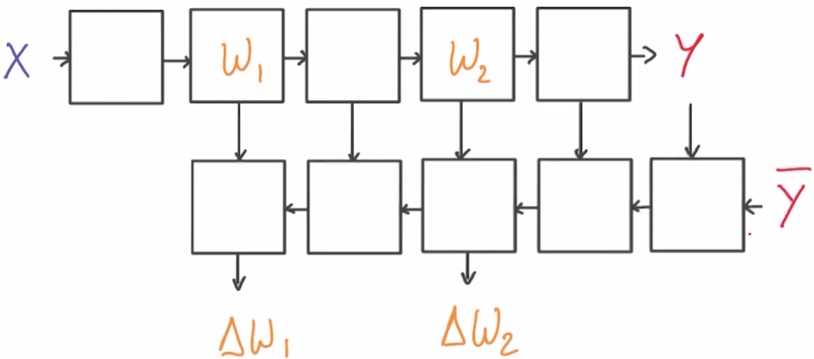
为了计算相应的偏导数 我们又画出了新的流程图来演示如何运算,数据在新图中的流动方向与之前的方向相反,
它集成了我们刚演示的链式法则来计算出梯度,这个图,可以完全自动地从你神经网络中每一个单独的运算出导出
大多数深度学习框架,都将会为我们完成这项工作
这就叫做反向传播法(back-propagation),是一个非常强大的概念
在函数是由由简单导数的函数复合而成的时候,该方法使得计算函数偏导数的过程变得非常高效
运行该模型进行预测的过程一般被称为 正向传播
而当模型反向运行以计算偏导数的时候 则被称为 逆向传播
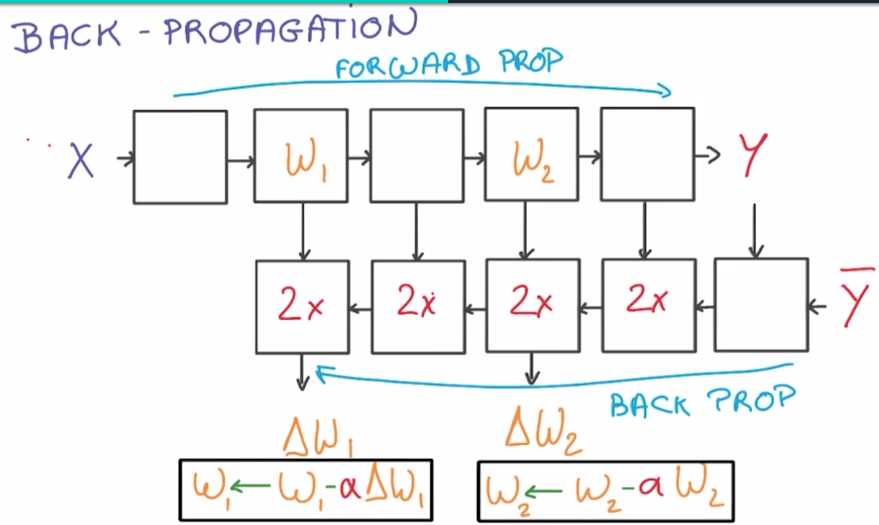
让我们来总结一下,在使用梯度下降法时,对训练集中的每一小批数据,你先后要运行正向、逆向传播
如此,你将会求出你模型各个权重的梯度值,然后,你就可以在原始的权重上,使用求出的梯度值和学习率来更新它
你将会重复该过程一次又一次,而这 就是你的模型变得优化的全部过程。
这里不展开讲每一步运算背后具体的运算过程,因为,通常不需要担心那些问题
因为它的核心就是链式法则,不过要记住,这个流程图,特别是逆向传播中的每个区块,
相比正向传播,它们通常需要花费两倍的运算与储存空间
当你需要改变你模型尺寸,并放到内存中的时候,这将会非常重要
原文:http://www.cnblogs.com/custer/p/6349505.html