效率爆表的一个晚上，只是因为没带手机，可怕！
今天开启新的课程，http://cs224d.stanford.edu/syllabus.html 第一章是凸优化，convex Optimazition
凸集 Convex Set
定义：
A set C is convex if, for any x, y ∈ C and θ ∈ R with 0 ≤ θ ≤ 1,
θx + (1 ? θ)y ∈ C.
判别方法：如果一个集合C是凸集，则C中任意两个元素连线上的点都属于C
举例：所有的实数空间；实数空间的非负实数域；
凸方程 Convex Function
定义：定义域D(f)为凸集，且对于任意两个属于D(f)的两个数x,y ； θ ∈ R, 0 ≤ θ ≤ 1,满足
f(θx + (1 ? θ)y) ≤ θf(x) + (1 ? θ)f(y).
first-order approximation：
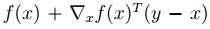
first order condition for convexity
当且仅当 D(f)是凸集且对于所有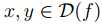
满足
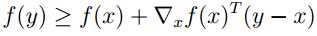
则f 是凸方程
second order condition for convexity ：
当且仅当 D(f)是凸集且f的海瑟Hessian矩阵（二阶导复合）是半正定：
x ∈ D(f),
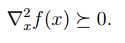
Jensen’s Inequality
将凸函数的定义扩展到多个点
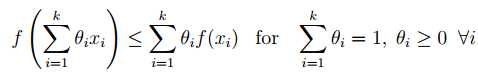
若扩展为积分
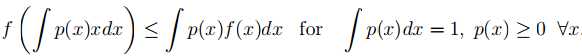
设定为概率密度
f(E[x]) ≤ E[f(x)]
即为Jensen‘s Inequality
α-Sublevel Sets
定义：对于凸函数f和α ∈ R，{x ∈ D(f) : f(x) ≤ α}
凸集：f(θx + (1 ? θ)y) ≤ θf(x) + (1 ? θ)f(y) ≤ θα + (1 ? θ)α = α
Convex Optimization Problems
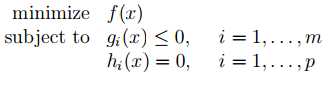
where f is a convex function, gi are convex functions, and hi are affine functions, and x is the optimization variable
affine function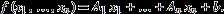 
optimal value
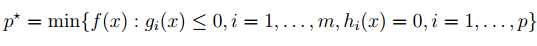
locally optimal if there are no “nearby” feasible points that have a lower objective value
globally optimal if there are no feasible points at all that have a lower objective value
在凸优化问题中，所有的局部最优都是全局最优
凸优化中的特例
Linear Programming
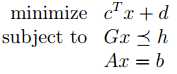
Quadratic Programming
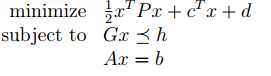
Quadraticallly Constrained Quadratic Programming
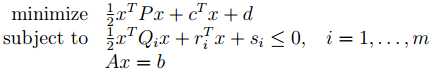
Semidefinite Programming
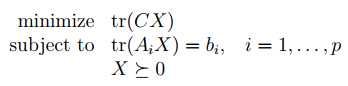
Support Vector Machines 是凸优化中一个典型应用
两类样本中离分类面最近的点且平行于最优分类面的超平面上H1,H2的训练样本就叫做支持向量
问题描述：
假定训练数据 ：
可以被分为一个超平面：
进行归一化：
此时分类间隔等于：
即使得：最大间隔最大等价于使
最小
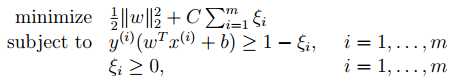
Constrained least squares
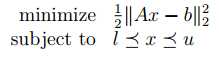
Maximum Likelihood for Logistic Regression
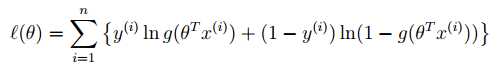
minimize ?(θ)
应用：
Linear SVM using CVX
Deep Learning for Natural Language Processeing : Convex Optimization
原文：http://www.cnblogs.com/learnmuch/p/5965275.html