根据上一次推导出来的问题:

从计算的角度来说,如果维度太大,向量z的内积求解起来非常的耗时耗力。
我们可以把这个过程分拆成两个步骤,先是一个x空间到z空间的转换Φ,再在z空间里做内积。如果能把这两个步骤合起来算得快一点的话就可以避开这个大计算量。
x和x‘转换了再做内积:
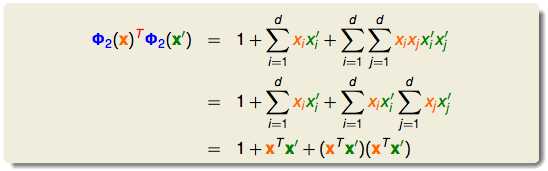
这样的方法可以算得比较快,因为直接在x空间内计算就好了,不用在z空间计算:

而这样的转换叫做kernel function:
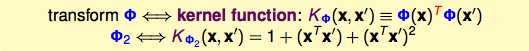
这个kernel在SVM里怎样应用呢?

可见,kernel trick是一个避免了在高纬度空间进行计算的方法。根据上图的替代,得出了kernel SVM:

而且,kernel SVM在做prediction的时候只需要SV就可以了。
下面介绍更多的其他形式的二项式转换的kernel:
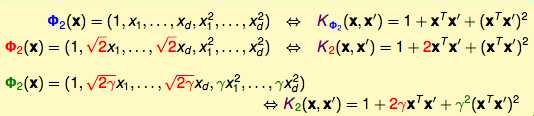
上面的放缩可以提炼成更加通用的形式:
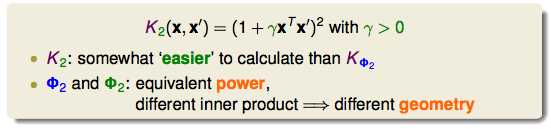

只要稍微改一下kernel,点对我们要找的线的距离也会随之改变(distance/margin),SV也会跟着改变。所以kernel也要仔细选择。
从2次项kernel,往高次项kernel推导:
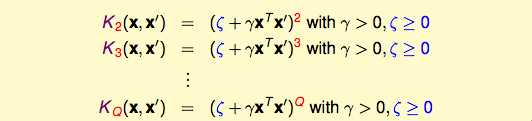
不管是什么样的维度,kernel的好处都是适用的:

kernel做1维转换的时候:
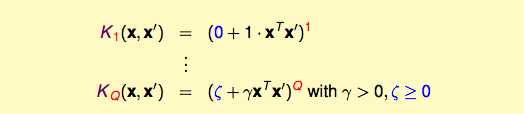
这样简单的转换用原来的方法解决就好了。
那如果这个维度是无限大呢?

上图证明了无限多维的kernel也是可行的。所以引出了Gaussian kernel:

把它代入到SVM里:

得到了中心在SV上的线性函数。所以高斯kernel的本质是:

下面比较一下不同kernel的优缺点:
linear kernel

polynomial kernel

Gaussian kernel

其他kernel的介绍:

kernel代表了向量的内积,也就是向量的相似性。kernel必须具备两个特质,一个是对称性,另一个是半正定。
总结:

机器学习技法(3)--Kernel Support Vector Machine
原文:http://www.cnblogs.com/cyoutetsu/p/5920629.html