matlab中各种高斯相关函数
最常见的是产生服从一维标准正态分布 的随机数
的随机数
实现服从任意一维高斯分布的随机数
- u=10;
- sigma=4;
- x=sigma*randn(1,n)+u
产生服从多元高斯分布的随机变量 函数mvnrnd,[multivarite normal random]
函数mvnrnd,[multivarite normal random]
- n=100;
- mu=[1 -1];
- Sigma=[.9,.4;.4,.3];
- r=mvnrnd(mu,Sigma,n);
将产生的随机数绘制在二维平面
当然mvnrnd函数还可以产生更高维数的高斯随机数,具体参见matlab help。
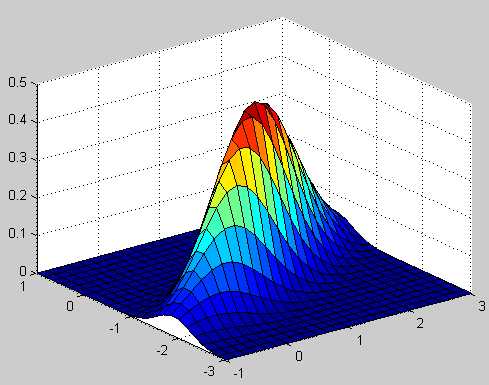
产生多元高斯分布概率密度函数
Y=mvnpdf(X,[MU,Sigma])
其中可省参数MU,Sigma默认值分别为零向量和单位阵,X是 的矩阵,N是样本个数,D是样本维数。
的矩阵,N是样本个数,D是样本维数。
- mu = [1 -1]; Sigma = [.9 .4; .4 .3];
- [X1,X2] = meshgrid(linspace(-1,3,25)‘, linspace(-3,1,25)‘);
- X = [X1(:) X2(:)];
- p = mvnpdf(X, mu, Sigma);
- surf(X1,X2,reshape(p,25,25));
和下面代码产生的趋势相同
- mu = [1 -1];
- Sigma = [.9 .4; .4 .3];
- [X,Y] = meshgrid(linspace(-1,3,25)‘, linspace(-3,1,25)‘);
- for i=1:25
- for j=1:25
- XY=[X(i,j),Y(i,j)];
- Z(i,j)=exp(-0.5*(XY-mu)/Sigma*(XY-mu)‘);
- end
- end
- surf(X,Y,Z);
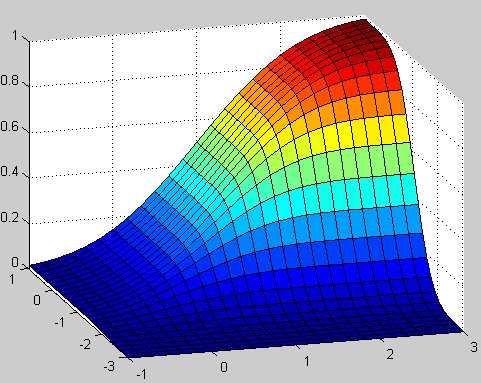
高斯分布函数
Y=mvncdf(X,[Mu],[Sigma]) , cumulative probability of the multivariate norm distribution with mean Mu and covariance Sigma.
具体使用看代码
- mu = [1 -1]; Sigma = [.9 .4; .4 .3];
- [X1,X2] = meshgrid(linspace(-1,3,25)‘, linspace(-3,1,25)‘);
- X = [X1(:) X2(:)];
- p = mvncdf(X, mu, Sigma);
- surf(X1,X2,reshape(p,25,25));
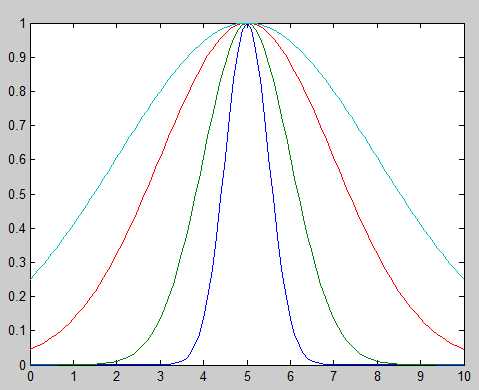
高斯隶属函数
gaussmf(X,[Sigma,Mu])
- x = (0:0.1:10)‘;
- y1 = gaussmf(x, [0.5 5]);
- y2 = gaussmf(x, [1 5]);
- y3 = gaussmf(x, [2 5]);
- y4 = gaussmf(x, [3 5]);
- plot(x, [y1 y2 y3 y4]);
 的随机数
的随机数
 函数mvnrnd,[multivarite normal random]
函数mvnrnd,[multivarite normal random]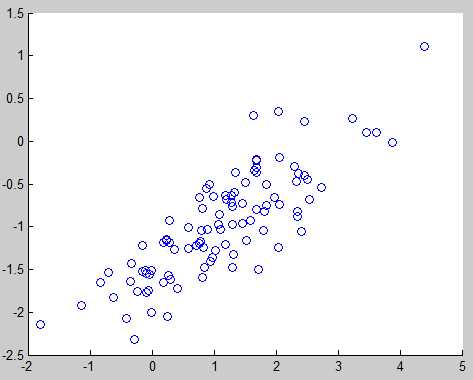
 的矩阵,N是样本个数,D是样本维数。
的矩阵,N是样本个数,D是样本维数。