数学函数

函数式编程背后的动力

函数式编程背后的动力来源自数学，数学函数拥有很多不错的特色，函数化语言试图现实世界中模拟。

首先，我们以为一个数添加1的函数开始。

Add1(x) = x+1

它是什么意思呢？它似乎很简单，这意味着有一个操作，为一个数字加1。

我们先解释一些术语

•  可以作为函数的输入的值的集合被称为域(domain)，在这个例中，它可以是一组真实的数字，现在为了更加简单，我们限制它只能是整数。
• 函数可能的输出值的集合被称为范围(range)【严格来说，是图片中的取值范围】。在这个例子中，我们也限制它只能是整数。
• 该函数被称为映射(map)域到范围。

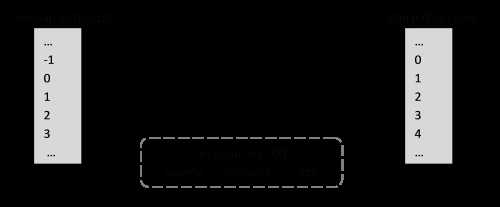
在F#中定义是这样的：

let add1 x = x + 1

如果你在F#中的即使窗口输入（不要忘记双分号） ，就会看到结果（函数的签名）：

val add1 : int -> int

我们仔细看一下输出：

• 总的来说是：“这个add1函数映射整数（域 domain）到整数（范围 range）”
• add1定义为“val”,"value"的简写，嗯。。。。它是什么意思呢？我们很快就会讨论到值。
• 箭头符号“->”用来表示从（域 domain）到（范围 range）在这个例子中，域是 int类型，范围也是int类型。

注意类型没有被指定，但F #编译器猜测函数正在为整数服务。（这能改变吗？是的，因为我们会看到不久的）

数学函数的关键特性

数学函数中的一些特性与你之前在编程中的特性不一样。

• 一个输入值函数总是会给出一个相同的输出值
• 函数没有副作用

这些属性提供了一些非常强大的好处，因此函数式编程语言试图在他们的设计中执行这些属性。让我们轮流看他们的每一个。

一个输入值函数总是会给出一个相同的输出值

在命令式编程中，我们认为函数是在“do 做”或者“calculate 计算”。数学函数不做任何的计算，只是单纯的从输入映射到输出。事实上，另一种简单的定义函数是所有映射的集合。例如，我们可以在C#中简陋的定义这个“add1”函数：

int add1(int input)
{ 
   switch (input)
   {
   case 0: return 1;
   case 1: return 2;
   case 2: return 3;
   case 3: return 4;
   etc ad infinitum
   }
}

很显然，我们不能为每个可能值都添加一个分支，但是原则上是一样的。你可以看过绝对没有任何的计算，只是查找。

函数没有副作用

在数学函数中，输入和输入在逻辑上是两个不同的东西，它们都是预定义的。函数不能改变输入和输出-它只是从域中预存在的值映射到范围中一个预存在的值。

换句话说，计算这个函数不能对输入有任何的影响或者任何其他事情。记住，计算这个函数不是实际的计算或者操纵任何事，只是查找。

值的“不变性”很微妙但是很重要。如果我在做数学，我不希望在我加的时候改变我的数字，例如，如果我这样：

x = 5
y = x+1

我不希望当我给x加什么数的时候x改变。我希望返回一个y，x原封不动。在数学的世界中，整数作为一个不可改变的集合已经存在，“add1”函数简单的定义他们之间的关系。

纯函数的力量

重复结果而且无副作用的函数称为“纯函数”，我们可以用它们做一些有意思的事

• 他们一般是并行的，我可以用从1到1000的整数，说，给我1000个不同的CPU，我可以同时在每个CPU上给对应的整数执行“add1”函数，安全方面，它们不需要相互作用。不需要锁，互斥锁，信号量等。
• 我可以用一个延迟函数，只有当我需要输出的时候计算。不管我计算的早或者晚，我可以确定答案是一致的。
• 我只需要计算一个函数一次特定的输入，而且我可以把它缓存起来，因为我知道同样的输入会给出同样的输出。
• 如果我有大量的纯函数，我可以任意顺序的执行它们。下次，它们的结果也不会有不同。

所以你可以看到如果我们用编程语言构造一个纯函数，我们立即就会获取很多强大的技能。事实上，你可以做用F#做所有的事：

• 你已经在“”系列中看到并行的例子了
• 计算延迟函数在“”系列中讨论
• 缓存函数结果叫做“memoization 备忘”也将在“”系列中讨论
• 不关注计算顺序使并发编程更简单，而且当函数调整顺序或者重构都不会引入bug

数学函数"无益的"特性

当用在编程的时候，数学函数也有一些看起来不是很好的特性。

• 输入和输出的值是不可变的
• 函数总是存在一个输入的一个输出

这些特性也反映在函数式编程语言上，让我们一个个的看看：

输入和输出的值是不可变的

不可变的值在理论上不错的想法，但在实际上如果你不能以传统的方式分配给变量，你怎么能完成工作？

我可以向你保证,这不是像你想的那个问题。当你通过这一系列的学习,你会看到在实践中是如何工作的。

函数总是存在一个输入的一个输出

像你看到的图解那样，数学函数总是只有存在一个输入和一个输出。这对于函数式编程语言也是的，尽管当你第一次用它的时候可能还不明显。

这看起来像是一个大烦恼。没有函数有两个（或者更多）参数你怎么做有用的事情？

当然，它变化了，有一个方法可以解决它，而且在F#中是完全透明的。它叫做“柯里化”，会很快出现在接下来的文章中。

事实上，你晚些就会发现，这两个没有用的特性变得非常的有用，而且这也是使函数式编程很强大的关键。

翻译有误，请指正，谢谢！

原文地址：http://fsharpforfunandprofit.com/posts/mathematical-functions/

数学函数

原文：http://www.cnblogs.com/JayWist/p/5847761.html