假如你想通过过去的天气,是否周末,是否促销三个属性和销量的关系来预测将来的销量的高低,这时你就可以通过以前的数据,选择这三个属性,通过计算信息熵的值来进行排序,对样本进行划分。这样就可以形成树状图了
5.具体建立决策树的步骤:
a)计算总的信息熵
b)计算每个测试属性的信息熵
c)计算天气,是否周末和是否促销属性的信息增益值
信息增益值=总的信息熵-测试属性的信息熵
d)针对每一个分支节点继续进行信息增益的计算,如此反复,直到没有新的节点分支,最终形成一棵决策树
e)当有新的样本进来就可以利用这颗决策树进行预测
6.补充————信息熵的计算
信息增益基于香浓的信息论,它找出的属性R具有这样的特点:以属性R分裂前后的信息增益比其他属性最大。这里信息的定义如下:
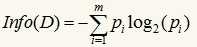
其中的m表示数据集D中类别C的个数,Pi表示D中任意一个记录属于Ci的概率,计算时Pi=(D中属于Ci类的集合的记录个数/|D|)。Info(D)表示将数据集D不同的类分开需要的信息量。
举例:
a)比如我们将一个立方体A抛向空中,记落地时着地的面为f1,f1的取值为{1,2,3,4,5,6},
f1的熵entropy(f1)=-(1/6*log(1/6)+…+1/6*log(1/6))=-1*log(1/6)=2.58;
b)现在我们把立方体A换为正四面体B,记落地时着地的面为f2,f2的取值为{1,2,3,4},
f2的熵entropy(1)=-(1/4*log(1/4)+1/4*log(1/4)+1/4*log(1/4)+1/4*log(1/4)) =-log(1/4)=2;
c)如果我们再换成一个球C,记落地时着地的面为f3,显然不管怎么扔着地都是同一个面,即f3的取值为{1},
故其熵entropy(f3)=-1*log(1)=0。
结论:可以看到面数越多,熵值也越大,而当只有一个面的球时,熵值为0,此时表示不确定程度为0,也就是着地时向下的面是确定的。