最短路径中的松弛技术

松弛(relaxation):指对于图 G = (V, E) 中 每个顶点v ∈ V，都设置一个属性dist[v]，用来描述从源点s到v的最短路径上权值的上界.在开始进行一个最短路径算法时,只知道图中边和权值.随着算法的进行,逐渐得到各对顶点的最短路径的信息.算法会逐渐更新这些信息,每步都会检查是否可以找到一条路径比当前给定路径更短.这一过程通常称为松弛.

下面这两张图即为松弛操作.源点为点 S, 这里用 dist[i] 表示点 i 到源点 S 的最短路径,现对于边权为 60 的边 <u, v>进行松弛操作,如第一副图所示,现到顶点 v, u的最短路径分别为 100 和 30, 那么 dist[v] > dist[u] + W<u, v>, 所以对于 dist[v] 需要更新,则 S 到 v 的最短路径为 S 到 u 的最短路径经过<u, v>到 v.

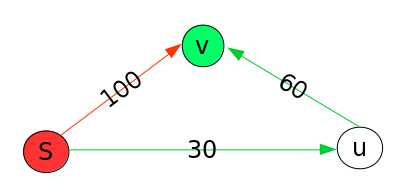
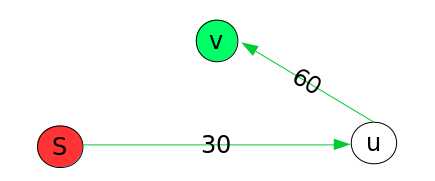
如上所述,则 dist[v] = dist[u] + W<u, v>.写成伪代码:

1 Relax( u,  v,  W<u, v> ) {//W<u, v>代表边<u, v> 的权值
2     if ( dist[v] > dist[u] + W<u, v> ) {
3         dist[v] = dist[u] + W<u, v>; 
4     }
5 }

最短路径中的松弛技术

原文：http://www.cnblogs.com/Ash-ly/p/5789746.html