·输出一个杨辉三角:
杨辉三角的性质:
每行数字左右对称,由1开始逐渐变大,然后变小,回到1。
第n行的数字个数为n个。
第n行的数字和为2^(n-1)。
每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角形。
第n行的第一个数为1,第二个数为1*(n-1),第三个数为1*(n-1)*(n-2)/2,第四个数为1*(n-1)*(n-2)/2*(n-3)/3...以此类推。
public class YangHuiSanJiao {
public static void main(String[] args) {
int[][] a = new int[10][10];
for (int i = 0; i < 10; i++) {
a[i][i] = 1;
a[i][0] = 1;
}
for (int i = 2; i < 10; i++) {
for (int j = 1; j < i; j++) {
a[i][j] = a[i - 1][j - 1] + a[i - 1][j];
}
}
for (int i = 0; i < 10; i++) {
for (int k = 0; k < 2 * (10 - i) - 1; k++) {
System.out.print(" ");
}
for (int j = 0; j <= i; j++) {
System.out.print(a[i][j] + " ");
}
System.out.println();
}
}
}
·算法:
使用一个二维数组yh[][]储存杨辉三角形的数据,行和列的大小为所需要输出的行数。
使用for循环实验室三角中除了最外层,(不包括底边)的数为1;
使用语句yh[i][j]=yh[i - 1] + yh[i - 1][j]使第i行第j列的数据等于第(i-1)行第(j-1)列的数据与第(i-1)行第(j)列的数据之和,即每个数字等于上一行的左右两个数字之和。
·输出结果如下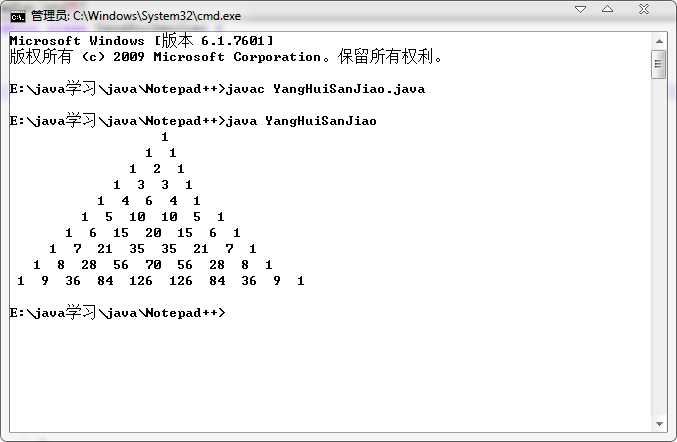
原文:http://www.cnblogs.com/sheril/p/5754713.html