给出m(m<=10)个长度不超过10的‘A‘‘T‘‘G‘‘C‘序列,求长度为n(n<=2*1e9)的‘A‘‘T‘‘G‘‘C‘序列不含上述m个序列中的任意一个序列的种类数。
首先出现了多个模板串,考虑Aho-Corasick,n的范围提示出要使用log级别的算法,并且能在Trie树上使用,矩阵是很好的选择,矩阵在有向图中的意义,可以求出s-t的方法数,因为矩阵的计算过程刚好满足乘法原理和加法原理,i行j列表示,i-j的方法数,例如以下矩阵
|0,1,1,0|
|0,0,0,1|这个矩阵就表示以下图形,
|0,1,0,1|如果问从i,走到j走N步的方式,
|0,0,0,0|那么就只需要矩阵n次幂,并输出i行j列的数字
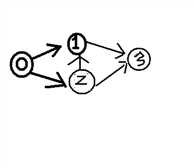
然而Aho-Corasick实在Trie上实现的,而Trie是一个有向的图(树),那么就构建矩阵,并输出root节点编号的矩阵那一行的总和。在得到fail指针的时候要把整个图建好。
#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <queue>
#include <cstring>
#include <algorithm>
#define LL long long//***
using namespace std;
const int N = 110;
const int mod = 100000;
int n,m,ncnt;
char ill[15];
struct node{
int id;
bool flag;
node *ch[4],*fail;
void init(){
flag = false;
for(int i = 0;i < 4;++i)ch[i] = NULL;
}
}trie[N*N];
int hash[128];//***
struct Matrix{
LL map[N][N];
void clear(){
memset(map,0,sizeof(map));
}
}c;
node *newnode(){
node *p = &trie[ncnt];
p->init();
p->id = ncnt++;
return p;
}
void insert(node *root,char *s){
node *p = root;
while(*s != ‘\0‘){
if(p->ch[hash[*s]])p = p->ch[hash[*s]];
else {
p->ch[hash[*s]] = newnode();
p = p->ch[hash[*s]];
}
++s;
}
p->flag = true;
}
void Build(node *root){
queue <node *> q;
q.push(root);
while(!q.empty()){
node *p = q.front();q.pop();
for(int i=0;i<4;++i){
if(p->ch[i]){
node *next = p->fail;
while(next && !next->ch[i])next = next->fail;
p->ch[i]->fail = next ? next->ch[i]:root;
if(p->ch[i]->fail->flag)p->ch[i]->flag=true;//***
q.push(p->ch[i]);
}
else p->ch[i] = (p == root) ? root:p->fail->ch[i];
if(!p->ch[i]->flag)++c.map[p->id][p->ch[i]->id];
}
}
}
Matrix Matrix_mul(Matrix x,Matrix y){
Matrix res;
res.clear();
for(int i = 0;i < ncnt;++i){
for(int j = 0;j < ncnt;++j){
for(int k = 0;k < ncnt;++k){
res.map[i][j] = (res.map[i][j]+y.map[i][k]*x.map[k][j])%mod;
}
}
}
return res;
}
Matrix Pow(Matrix x,int n){
Matrix res;
res.clear();
for(int i = 0;i < ncnt;++i)res.map[i][i] = 1;
while(n){
if(n&1)res = Matrix_mul(res,x);
x = Matrix_mul(x,x);
n >>=1;
}
return res;
}
void _fre(node *p){
for(int i = 0;i < 4;++i){
if(p->ch[i])_fre(p->ch[i]);
}
free(p);
}
int main(){
hash[‘A‘] = 0,hash[‘C‘] = 1,hash[‘G‘] = 2,hash[‘T‘] = 3;
while(scanf("%d%d",&m,&n) != EOF){
ncnt = 0;
c.clear();
memset(trie,0,sizeof(trie));
node *root = newnode();
for(int i = 0;i < m;++i){
scanf("%s",ill);
insert(root,ill);
}
Build(root);
Matrix res = Pow(c,n);
LL ans = 0;
for(int i = 0;i < ncnt;++i){
ans += res.map[0][i];
ans %= mod;
}
cout<<ans<<endl;
// _fre(root);莫名RE
}
return 0;
}
poj 2778 (Aho-Corasick & 矩阵优化) - xgtao -
原文:http://www.cnblogs.com/xgtao984/p/5701601.html