基于我们最为熟悉的离散型分布——二项分布,我们能够衍生出很多别的分布列,对于之前介绍过的几何分布,我们赋予其的含义是:某个事件成功的概率是p,在n次独立重复实验中恰好成功一次的概率是多少。顺着这层含义,我们把1次编程r次,便得到了所谓的负二项分布。设负二项分布的随机变量是X,独立事件成功的概率是p,则在n次重复独立实验中恰好成功r次的概率是:
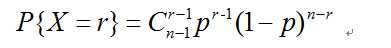
较之二项分布,我们能够看到,负二项分布更加强调n次重复实验中“恰好”成功r次,也就是要求第n次实验恰好是第r次成功的实验。
我们通过一个问题来进行举例——巴拿赫火柴问题。
Q:某个抽烟的数学家总是随身带着两盒火柴,一盒放在左边口袋一盒放在右边口袋。每次他需要火柴时,他就从任意的口袋中的火柴盒中取出一个火柴,现在两盒火柴中都各有N个火柴,那么请问他第一次发现其中一个盒子已经空了的时候,另一盒恰好有k根火柴的概率有多大?
分析:首先我们需要讨论的一个点是,这个火柴位于哪个口袋的火柴盒是空的,显然是左是右具有对称性,我们分析一种情况,进行平方即可。
假设左口袋为空,那么这个过程的最后一个步骤显然是在数学家第2N-k次取火柴的时候,必然取走了右口袋中的一根火柴,这是一位他拿走左口袋的最后一根火柴的时候,我们就可以默认理性的数学家不会再去拿左口袋的火柴盒,因此我们就可以将其与负二项分布联系起来:在2N-k次重复实验当中,恰好有N次从左口袋取出的概率。
即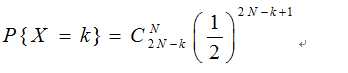
当然,这个问题的最终结果应该将如上的概率平方。
《A First Course in Probability》-chaper4-离散型随机变量-负二项分布
原文:http://www.cnblogs.com/rhythmic/p/5677240.html