| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 8857 | Accepted: 5740 |
Description
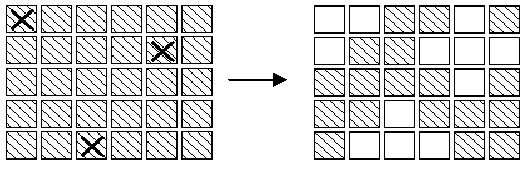
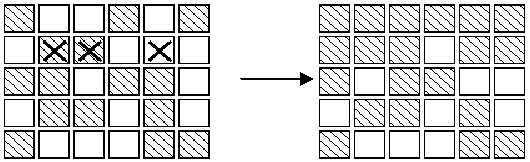
Input
Output
Sample Input
2 0 1 1 0 1 0 1 0 0 1 1 1 0 0 1 0 0 1 1 0 0 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 0
Sample Output
PUZZLE #1 1 0 1 0 0 1 1 1 0 1 0 1 0 0 1 0 1 1 1 0 0 1 0 0 0 1 0 0 0 0 PUZZLE #2 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 1 1 0 1 1 0 1
Source
有一个5*6的矩阵,每个方格代表一个灯,每操作一个灯,周围的上下左右四个灯会发生相应变化 即由灭变亮,由亮变灭,如何操作使灯全灭,并输出操作矩阵(1表示按,0表示不按)
解题思路:
其实这个题目跟上一个题目很类似(这个题目比上一个更简单),因为最后是让我们输出矩阵,而且根据题目意思来说,根本没有自由变元,也就是这个矩阵直接就是确定的,唯一解,然后我们构造一个A矩阵,跟上一个一样构造,然后直接套模板就行了。
My Code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
using namespace std;
const int MAXN = 1e2+5;
int equ, var;///equ个方程 var个变量
int a[MAXN][MAXN];///增广矩阵
int x[MAXN];///解的数目
bool free_x[MAXN];///判断是不是自由变元
int free_num;///自由变元的个数
inline int GCD(int m, int n)
{
if(n == 0)
return m;
return GCD(n, m%n);
}
inline int LCM(int a, int b)
{
return a/GCD(a,b)*b;
}
int Gauss()
{
int Max_r;///当前列绝对值最大的存在的行
///col:处理当前的列
int row = 0;
int free_x_num;
int free_index;
for(int col=0; row<equ&&col<var; row++,col++)
{
Max_r = row;
for(int i=row+1; i<equ; i++)
if(abs(a[i][col]) > abs(a[Max_r][col]))
Max_r = i;
if(Max_r != row)
for(int i=0; i<var+1; i++)
swap(a[row][i], a[Max_r][i]);
if(a[row][col] == 0)
{
row--;
continue;
}
for(int i=row+1; i<equ; i++)
{
if(a[i][col])
{
for(int j=col; j<var+1; j++)
a[i][j] ^= a[row][j];
}
}
}
for(int i=row; i<equ; i++)
if(a[i][var])
return -1;///无解
if(row < var)
{
for(int i=row-1; i>=0; i--)
{
free_x_num = 0;
for(int j=0; j<var; j++)
if(a[i][j] && free_x[j])
{
free_x_num++;
free_index = j;
}
if(free_x_num > 1)
continue;
int tmp = a[i][var];
for(int j=0; j<var; j++)
if(a[i][j] && j!=free_index)
tmp -= a[i][j]*x[j];
x[free_index] = tmp/a[i][free_index];/// 求出该变元.
free_x[free_index] = 0; /// 该变元是确定的.
}
return var - row;///自由变元的个数
}
for(int i=var-1; i>=0; i--)
{
int tmp = a[i][var];
for(int j=i+1; j<var; j++)
if (a[i][j])
tmp ^= a[i][j]*x[j];
if (tmp%a[i][i])
return -2; /// 说明有浮点数解,但无整数解.
x[i] = tmp/a[i][i];
}
return 0;///唯一解
}
int main()
{
int T;
cin>>T;
for(int cas=1; cas<=T; cas++)
{
memset(a, 0, sizeof(a));
memset(x, 0, sizeof(x));
equ = var = 30;
for(int i=0; i<var; i++)
{
int ta = i%6, tb = i/6;
a[i][i] = 1;
if(ta > 0)
a[i][i-1] = 1;
if(ta < 5)
a[i][i+1] = 1;
if(tb > 0)
a[i][i-6] = 1;
if(tb < 5)
a[i][i+6] = 1;
}
for(int i=0; i<equ; i++)
cin>>a[i][var];
int k = Gauss();
printf("PUZZLE #%d\n",cas);
for(int i=0; i<var; i++)
{
if(i%6 == 5)
cout<<x[i]<<endl;
else
cout<<x[i]<<" ";
}
}
return 0;
}
POJ 1222 EXTENDED LIGHTS OUT(高斯消元)
原文:http://blog.csdn.net/qingshui23/article/details/51693943