（整理自AndrewNG的课件，转载请注明。整理者：华科小涛@http://www.cnblogs.com/hust-ghtao/）
SVM有点让人头疼，但还是要弄明白。把这一大块搞懂了，会很有成就感的哦！今天先不谈SVM，先来说一下如何解决带约束的优化问题。
假设我们有如下问题需要求解：
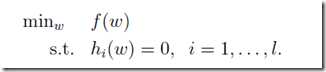，这是一个带有等式约束的优化问题，下面让我们用拉格朗日乘数法（THE Method of
Lagrange multipliers）来解决这个
问题，首先定义拉格朗日函数：
，其中
就被成为拉格朗日乘子，然后就令
的偏导分别为0就可求得参数：
。这种方法就是我们学过的用拉格朗日乘数法求函数的极值。
下面，让我们将这个问题扩展一下，引入不等式约束：
，同样我们定义更一般的拉格朗日函数：
，其中
和
称为拉格朗日乘子。
SVM(支持向量机)（二）—Lagrange Duality（拉格朗日对偶问题）,布布扣,bubuko.com
SVM(支持向量机)（二）—Lagrange Duality（拉格朗日对偶问题）
原文：http://www.cnblogs.com/hust-ghtao/p/3693137.html