节选自 汪林《实分析中的反例》
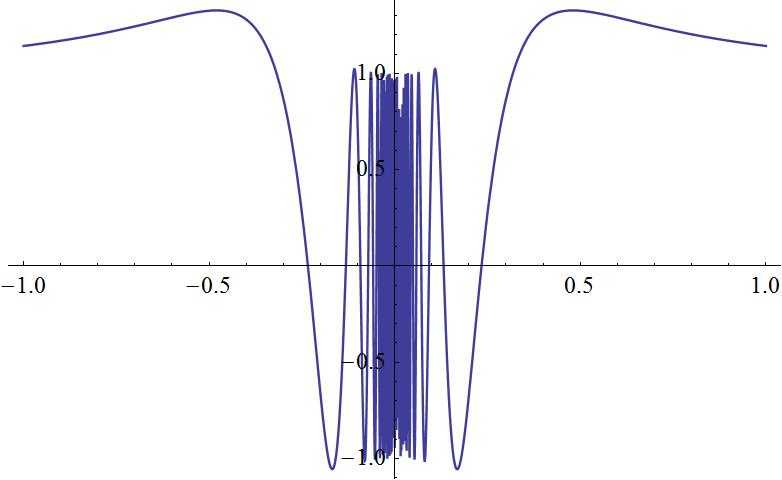
在$[0,1]$上定义函数
$$g(x)=x^{2}\sin \frac{1}{x}, x\neq 0$$
补充定义$g(0)=0$, 则函数$g(x)$为连续函数,图形如下。
导函数可求得
$$g‘(x)=2x\sin \frac{1}{x}-\cos \frac{1}{x},x \neq 0$$
并且$g‘(0)=0$, 所以$g‘(x)$在$x=0$处并不连续。导函数存在但并非$\mathbb{R}$上连续函数。
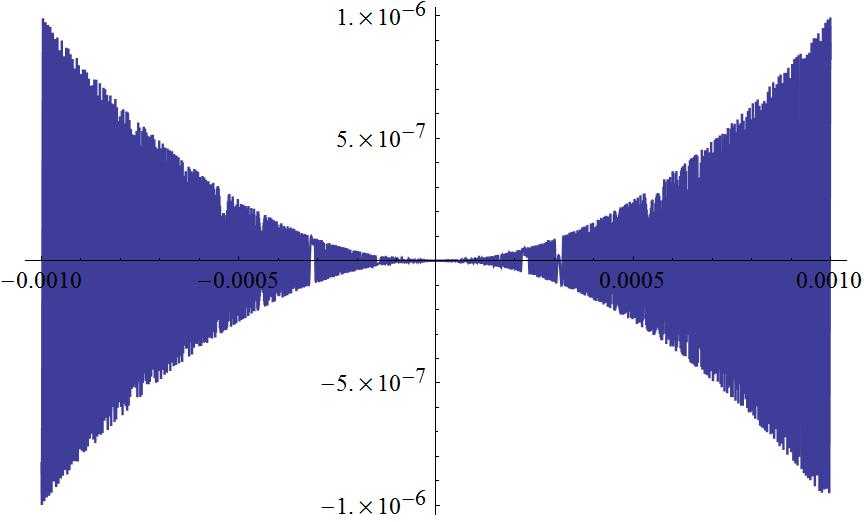
设$\{r_{n}\}$为闭区间$[0,1]$之间所有的有理数,则函数
$$f(x)=\sum_{n=0}^{\infty}\frac{1}{2^{n}}g(x-r_{n})$$
在$[0,1]$一致收敛
$$f‘(x)=\sum_{n=0}^{\infty}\frac{1}{2^{n}}g’(x-r_{n})$$
在$[0,1]$上的有理数点$r_{n}$上不连续,在$[0,1]$上的无理数点连续。
原文:http://www.cnblogs.com/zhangwenbiao/p/5426699.html