Lucas–Kanade光流算法是一种两帧差分的光流估计算法。它由Bruce D. Lucas 和 Takeo Kanade提出。
H.O.T. 指更高阶，在移动足够小的情况下可以忽略。从这个方程中我们可以得到：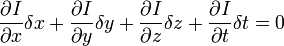
或者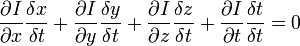
我们得到：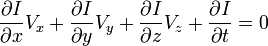
V x ,V y ,V z 分别是I(x,y,z,t)的光流向量中x，y，z的组成。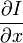 
, 
, 
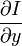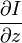和 
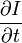则是图像在(x ,y ,z ,t )这一点向相应方向的差分 。
所以
I x V x + I y V y + I z V z = ? I t。
这个方程有三个未知量，尚不能被解决，这也就是所谓光流算法的光圈问题。那么要找到光流向量则需要另一套解决的方案。而Lucas-Kanade算法是一个非迭代的算法：
假设流(Vx,Vy,Vz)在一个大小为m*m*m(m>1)的小窗中是一个常数，那么从像素1...n , n = m 3 中可以得到下列一组方程：（也就是说，对于这多个点，它们三个方向的速度是一样的）即，假设了在一个像素的周围的一个小的窗口内的所有像素点的光流大小是相同的。
（
而两帧图像之间的变化，就是t方向的梯度值，可以理解为当前像素点沿着光流方向运动而得到的，所以我们可以得到上边的这个式子。令：
）
三个未知数但是有多于三个的方程，这个方程组自然是个超定方程，也就是说方程组内有冗余，方程组可以表示为：
这也就是说寻找光流可以通过在四维上图像导数的分别累加得出。我们还需要一个权重函数W(i, j,k) ，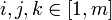 
来突出窗口中心点的坐标。高斯函数做这项工作是非常合适的，
这个算法的不足在于它不能产生一个密度很高的流向量，例如在运动的边缘和黑大的同质区域中的微小移动方面流信息会很快的褪去。它的优点在于有噪声存在的鲁棒性还是可以的。
补充：opencv里实现的看上去蛮复杂，现在还不是太明白。其中LK经典算法也是迭代法，是由高斯迭代法解线性方程组进行迭代的。
参考资料：http://www.cnblogs.com/gnuhpc/archive/2012/12/04/2802124.html
原文：http://www.cnblogs.com/dverdon/p/5325498.html
or