题目:返回一个整数数组中最大子数组的和。
要求:
结对编程要求:
分析:相比于上一次的任务,这次的不同在于,数组是环状的,求出所有可能子数组之和的最大值,并确定该子数组所在的位置。这时就会有两种想法:a想到环状,就想到了数据结构中的循环链表,balabala。。。。。b其实也不难,只是加入环状之后,每次搜索子数组的起点在变,终点也会变化。这时仅仅需要把每一种起点情况下的最大子数组之和S求出,存入S[]数组中,最后比较S[]中的最大值(i为数组的长度)存为MaxSum。而此时的起点-finalStart和终点-finalEnd也同样可以在求MaxSum的同时记录下来。最后输出结果。
代码实现如下:
//求数组中最大子序列的和 王世强 2016/3/24
#include<iostream>
using namespace std;
int main()
{
int Array[100],i=1,dp[100][2],j,MaxSum;
int s0=-1,e0=-1,s1=0,e1=0;
cout<<"请输入一组数组:";
cin>>Array[0];
while(getchar()!=‘\n‘) //输入数组部分,空格表示输入结束
{
cin>>Array[i++];
}
int S[i],start[i],end[i],n,finalStart,finalEnd;
for(n=0;n<i;n++)
{
dp[0][0]=0;
dp[0][1]=Array[n];
for(j=1;j<i;j++)
{
if(dp[j-1][0]<dp[j-1][1])
{
dp[j][0]=dp[j-1][1];
s0=s1,e0=e1;
}
else
{
dp[j][0]=dp[j-1][0];
}
if(Array[j]<(dp[j-1][1]+Array[(j+n)%i]))
{
dp[j][1]=dp[j-1][1]+Array[(j+n)%i];
e1=j+n;
}
else
{
dp[j][1]=Array[(j+n)%i];
s1=e1=j+n;
}
}
if(dp[j-1][0]>dp[j-1][1])
{
S[n]=dp[j-1][0];
start[n]=s0;
end[n]=e0;
}
else
{
S[n]=dp[j-1][1];
start[n]=s1;
end[n]=e1;
}
}
MaxSum=S[0];
finalStart=start[0];
finalEnd=end[0];
for(n=0;n<i;n++)
{
if(MaxSum<S[n])
{
MaxSum=S[n];
finalStart=start[n];
finalEnd=end[n];
}
}
cout<<"最大子数组为和:"<<MaxSum<<"\n最大子数组为:";
for(int q=finalStart;q<=finalEnd;q++)
{
cout<<Array[q%i]<<" ";
}
return 0;
}
运行结果截图:
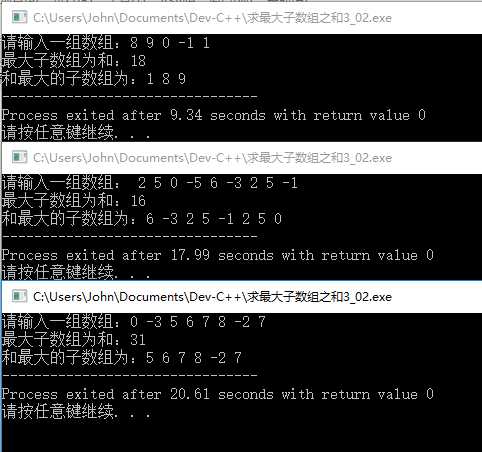
总结:团队开发还是效率挺高的,可以相互交流比较好的想法,相互学习。如果一个人单独思考,想法具有局限性,而且还可能特别花时间。
虚心学习,共同进步!
原文:http://www.cnblogs.com/wsqJohn/p/5316498.html