题目:http://acm.hust.edu.cn/vjudge/problem/viewProblem.action?id=13674
1.首先要明确货物必须要按照输入的顺序依次寄出,而且每一次携带有容量限制,所以可以理解成对于前n个货物的投递问题(dp[n]),我们要找一个任意合适的下标k,使得(k+1)~n的货物<容量限制,这时问题便化为:前k个货物的子问题的最优解(dp[k]) 加上 (k+1)~n的货物一趟来回运送的代价
有了上面的认识,就可以很轻松的列出动态转移方程了:
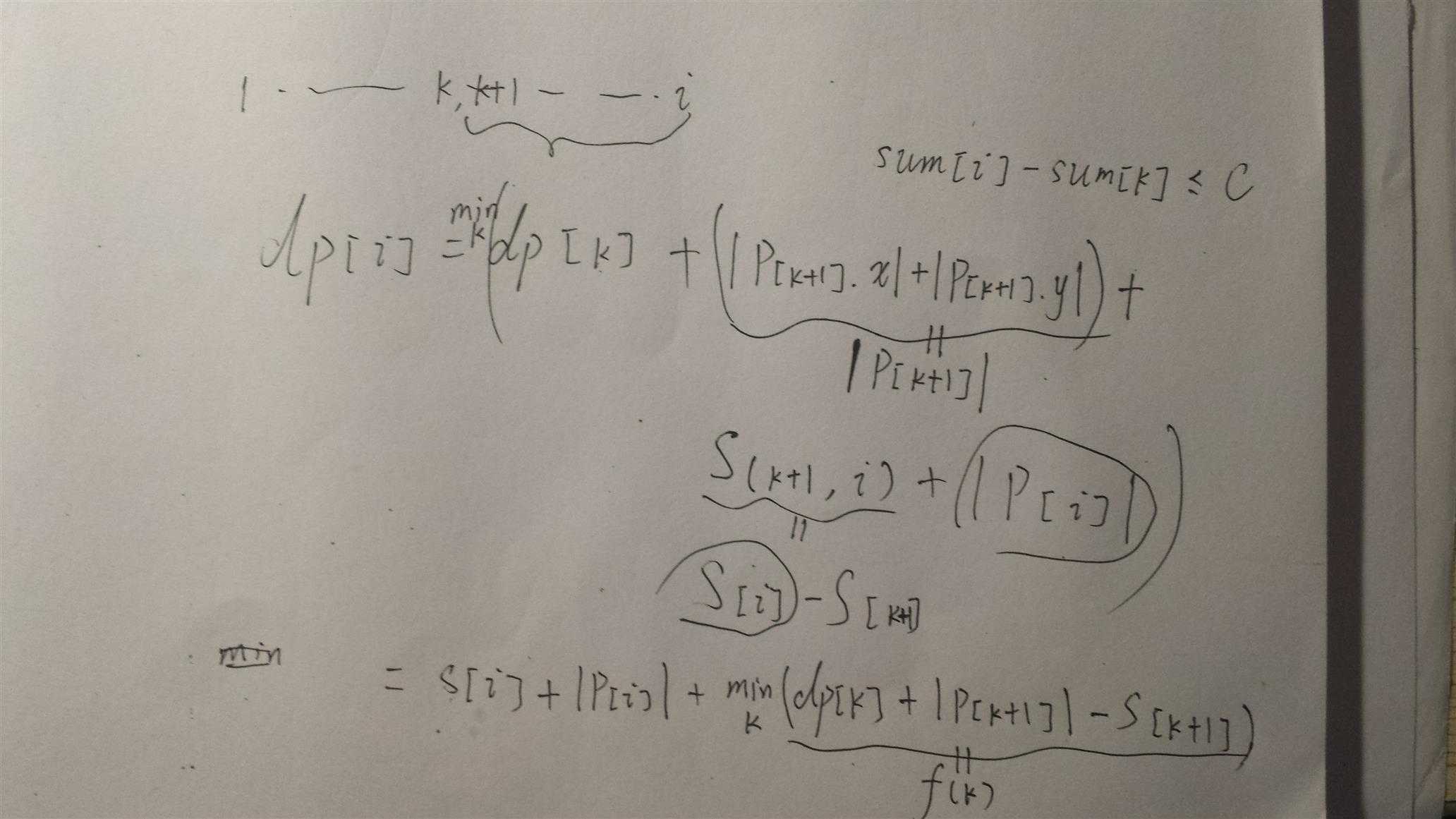
2. 然后,我们可以看到有i和k两个下标,所以貌似会有两重循环,然后N<=1e5,两重循环很难在3s内通过的,所以要想办法降低时间复杂度。
①我们可否通过从左到右遍历的时候动态维护一个当前最小的f(k) ?这样就不用第二重循环来找了呀!
②看似可以喔?但是我们会发现有一个很棘手的问题:我们有一个容量限制的额外条件!即,我们一直维护的最小值要是满足该条件的最小值,这一点对往常的“动态维护”策略造成了很大的麻烦。
③其实,我们可以通过一个数据结构,来动态维护它!该数据结构需要满足一下条件:1)可以增加、删除元素 2)求所有元素的最小值
有很多常用的数据结构可以满足这两个条件,然而《训练指南》给出了一个更好的数据结构,仅一个双端队列即可!
#include <cstdio> #include <iostream> #include <cmath> #include <queue> using namespace std; struct P{ int x, y; P(int x=0, int y=0):x(x),y(y) {} } p[100005]; int c[100005]; int S[100005]; int que[100005]; int dp[100005]; int f(int k) { return dp[k]+abs(p[k+1].x)+abs(p[k+1].y)-S[k+1]; } int main () { int T, C, N, w; scanf ("%d", &T); while(T--) { scanf("%d%d", &C, &N); for(int i=1; i<=N; i++) { scanf("%d%d%d", &p[i].x, &p[i].y, &w); c[i] = c[i-1] + w; S[i] = S[i-1] + abs(p[i].x-p[i-1].x) + abs(p[i].y-p[i-1].y); } int l=0, r=1, k; que[0] = 0; for(int i=1; i<=N; i++) { // [l , r) while(l<r && c[i] - c[que[l]] > C) ++l; k = que[l]; dp[i] = S[i] + abs(p[i].x)+abs(p[i].y) + f(k); while(l<r && f(que[r-1])>f(i)) --r; que[r++] = i; } printf("%d\n", dp[N]); if(T>0) printf("\n"); } return 0; }
原文:http://www.cnblogs.com/AcIsFun/p/5315026.html