返回一个整数数组中最大子数组的和

题目:返回一个整数数组中最大子数组的和。
要求：

• 输入一个整形数组，数组里有正数也有负数。
• 数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。
• 求所有子数组的和的最大值。要求时间复杂度为O(n)
• 发表一篇博客文章讲述设计思想，出现的问题，可能的解决方案（多选）、源代码、结果截图、总结。（截止时间周六3月26日晚18:00之前）

一开始看到题目我的第一感觉就是，挨个求出每个子数组的和，然后进行比较，这样的话有n个元素的数组就有n（n+1）/2个子数组，而且计算起来相当麻烦。然而这样时间复杂度是O（n^2)也不满足要求，正在我绞尽脑子想要解决这个问题时，我的同桌不到五分钟就把问题解决了，而且用了很少的代码。。。只想说他太厉害了，自己的差距太大。

听过他的解释，说要用到动态规划来解决此问题，会变得非常简单。于是照着他的思路，我编写了这个程序：

//求数组中最大子序列的和  王世强 2016/3/22 
#include<iostream>
using namespace std;
int main()
{
	int Array[100],i=1,dp[100][2],j,S;
	cout<<"请输入一组数组：";
	cin>>Array[0];
	while(getchar()!=‘\n‘)
	{
		cin>>Array[i++];
	}
	dp[0][0]=0;
	dp[0][1]=Array[0];
	for(j=1;j<i;j++)
	{
		dp[j][0]=max(dp[j-1][0],dp[j-1][1]);
		dp[j][1]=max(Array[j],(dp[j-1][1]+Array[j]));
	}
	S=max(dp[i-1][0],dp[i-1][1]);
	cout<<"最大子序列的和为："<<S;
	return 0;
 } 

　　这里解释一下，dp[i][0]和dp[i][1]。

dap[i][0]指前i个元素中，不包含Array[i]的子数组中和最大的值；dp[i][1]指前i个元素中，包含Array[i]的子数组中和最大的值。从第一个元素开始循环直至求出最后一对dp[i][0]和dp[i][1]，再比较其大小，输出最大的子数组之和。

运行结果截图如下：

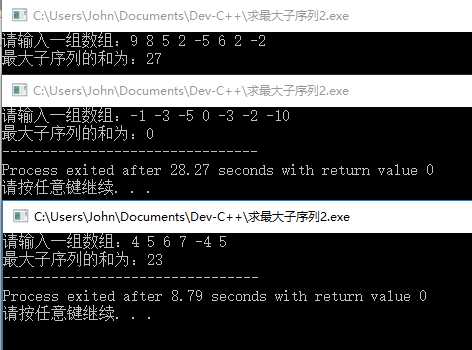
总结：感觉算法懂的太少，第一次听说在程序上用动态规划来解决问题，而且解决问题的效率真的很高，无论是从代码量还是时间复杂度上，都可以看出好的算法在解决问题上带来的方便。要多多努力才是！

返回一个整数数组中最大子数组的和

原文：http://www.cnblogs.com/wsqJohn/p/5308586.html