| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 4637 | Accepted: 2099 |
Description
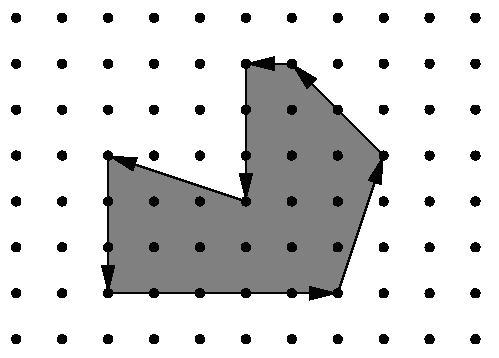
Input
Output
Sample Input
2 4 1 0 0 1 -1 0 0 -1 7 5 0 1 3 -2 2 -1 0 0 -3 -3 1 0 -3
Sample Output
Scenario #1: 0 4 1.0 Scenario #2: 12 16 19.0
复制一段讲解,慢慢理解。
S=a+ b/2 - 1
(其中a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积)
其实这个公式主要是用来求a的,s可由叉积得出,b可由gcd求出。
pick公式无比牛逼证明(感谢ldl提供出处)
Pick定理是说,假设平面上有一个顶点全在格点上的多边形P,那么其面积S(P)应该等于i+b/2-1,其中i为多边形内部所含的格点数,b是多边形边界上的格点数。绝大多数证明都是用割补的办法重新拼拆多边形。这里,我们来看一个另类的证明。
假设整个平面是一个无穷大的铁板;在0时间,每个格点上都有一个单位的热量。经过无穷长时间的传导后,最终这些热量将以单位密度均匀地分布在整个铁板上。下面我们试着求多边形P内的热量。考虑多边形的每一条线段e:它的两个端点均在格点上,因此线段e的中点是整个平面格点的对称中心,因而流经该线段的热量收支平衡(这半边进来了多少那半边就出去了多少),即出入该线段的热量总和实际为0。我们立即看到,P的热量其实完全来自于它自身内部的i个格点(的全部热量),以及边界上的b个格点(各自在某一角度范围内传出的热量)。边界上的b个点形成了一个内角和为(b-2)*180的b边形,从这b个点流入P的热量为(b-2)*180/360
= (b-2)/2 = b/2-1。再加上i个内部格点,于是S(P)=i+b/2-1。
/* ***********************************************
Author :rabbit
Created Time :2014/4/20 9:39:31
File Name :8.cpp
************************************************ */
#pragma comment(linker, "/STACK:102400000,102400000")
#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <sstream>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#include <string>
#include <time.h>
#include <math.h>
#include <queue>
#include <stack>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define eps 1e-10
#define pi acos(-1.0)
typedef long long ll;
int dcmp(double x){
if(fabs(x)<eps)return 0;
return x>0?1:-1;
}
struct Point{
double x,y;
Point(double _x=0,double _y=0){
x=_x;y=_y;
}
};
Point operator + (Point a,Point b){
return Point(a.x+b.x,a.y+b.y);
}
Point operator - (Point a,Point b){
return Point(a.x-b.x,a.y-b.y);
}
Point operator * (Point a,double p){
return Point(a.x*p,a.y*p);
}
Point operator / (Point a,double p){
return Point(a.x/p,a.y/p);
}
bool operator < (const Point &a,const Point &b){
return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
bool operator == (const Point &a,const Point &b){
return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;
}
double Dot(Point a,Point b){
return a.x*b.x+a.y*b.y;
}
double Length(Point a){
return sqrt(Dot(a,a));
}
double Angle(Point a,Point b){
return acos(Dot(a,b)/Length(a)/Length(b));
}
double angle(Point a){
return atan2(a.y,a.x);
}
double Cross(Point a,Point b){
return a.x*b.y-a.y*b.x;
}
Point vecunit(Point x){
return x/Length(x);
}
Point Normal(Point x){
return Point(-x.y,x.x);
}
Point Rotate(Point a,double rad){
return Point(a.x*cos(rad)-a.y*sin(rad),a.x*sin(rad)+a.y*cos(rad));
}
struct Line{
Point p,v;
double ang;
Line(){}
Line(Point P,Point v):p(P),v(v){
ang=atan2(v.y,v.x);
}
bool operator < (const Line &L) const {
return ang<L.ang;
}
Point point(double a){
return p+(v*a);
}
};
bool SegmentIntersection(Point a1,Point a2,Point b1,Point b2){
double c1=Cross(a2-a1,b1-a1),c2=Cross(a2-a1,b2-a1),
c3=Cross(b2-b1,a1-b1),c4=Cross(b2-b1,a2-b1);
return dcmp(c1)*dcmp(c2)<0&&dcmp(c3)*dcmp(c4)<0;
}
struct Node{
ll x,y;
}pp[100100];
ll gcd(ll a,ll b){
if(a==0)return b;
return gcd(b%a,a);
}
ll xmult(Node a,Node b){
return a.x*b.y-a.y*b.x;
}
int main()
{
ll n;
int T;
cin>>T;
for(int t=1;t<=T;t++){
cin>>n;
pp[0].x=pp[0].y=0;
for(int i=1;i<=n;i++){
ll x,y;
scanf("%lld%lld",&x,&y);
pp[i].x=pp[i-1].x+x;
pp[i].y=pp[i-1].y+y;
}
ll s=0,e=0,q;
for(int i=0;i<n;i++){
s+=xmult(pp[i],pp[i+1]);
ll dx=pp[i].x-pp[i+1].x;if(dx<=0)dx=-dx;
ll dy=pp[i].y-pp[i+1].y;if(dy<=0)dy=-dy;
e+=gcd(dx,dy);
}
if(s<=0)s=-s;
q=s/2+1-e/2;
printf("Scenario #%d:\n",t);
printf("%lld %lld %.1f\n",q,e,s/2.0);
puts("");
}
}
POJ 1265 pick定理,布布扣,bubuko.com
原文:http://blog.csdn.net/xianxingwuguan1/article/details/24272499