先把问题做最大程度的简化，（把复杂问题简化是理解的一种方式），在3*3的二维数组中模拟，此外，移动方向只包括向下移，和右移两种方式。先下移，再右移。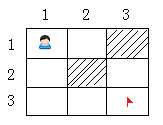
在这个二维数组中，约定规则：0表示通路，-1表示路径（可通过），1表示障碍物。于是得到一个二维数组的形式如下：（由于四周需要障碍物围墙，所以外围加了一层，即总共为：5*5的二维数组）
{ {1,1,1,1,1}, {1,0,0,1,1}, {1,0,1,0,1}, {1,0,0,0,1}, {1,1,1,1,1} }
由于只能下移和右移，这就很类似于二叉树的先序遍历，所以用递归形式：
if (maze[x + 1][y] == 0) //下移 pass(x + 1, y); if (maze[x][y + 1] == 0) //右移 pass(x, y + 1);
直接看图表示清晰：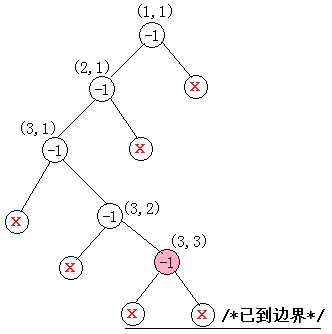
递归最后的约束条件为最后移动到的坐标=目标坐标，即是一种可行的方式。代码如下：
void pass(int x, int y) { maze[x][y] = -1; //初始设该位置可通过 if (x == OutX && y == OutY) //若已到终点 { printf("\n路径:\n"); PrintMaze(); } if (maze[x + 1][y] == 0) //下移 pass(x + 1, y); if (maze[x][y + 1] == 0) //右移 pass(x, y + 1); maze[x][y] = 0; //若该位置上下左右都没有路径，设置为不通 }
原文：http://www.cnblogs.com/tinaluo/p/5290216.html