【POJ 1699】 Best Sequence（KMP+状压DP）

【POJ 1699】 Best Sequence（KMP+状压DP）

Description

The twenty-first century is a biology-technology developing century. One of the most attractive and challenging tasks is on the gene project, especially on gene sorting program. Recently we know that a gene is made of DNA. The nucleotide bases from which DNA is built are A(adenine), C(cytosine), G(guanine), and T(thymine). Given several segments of a gene, you are asked to make a shortest sequence from them. The sequence should use all the segments, and you cannot flip any of the segments.

For example, given ‘TCGG‘, ‘GCAG‘, ‘CCGC‘, ‘GATC‘ and ‘ATCG‘, you can slide the segments in the following way and get a sequence of length 11. It is the shortest sequence (but may be not the only one).

Input

Output

Sample Input

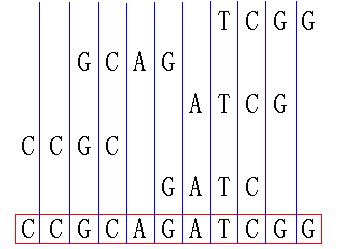
1
5
TCGG
GCAG
CCGC
GATC
ATCG

Sample Output

11

Source

题目大意：T组输入，对于每组输入先是一个正整数n，之后跟着n个串，每个串长度1~20不等。

问把这n个串串成一个长串至少需要多少个字符，连接方式可以是a串后缀与b串前缀相同时叠加方式连接。

由于串很少，可以想到状压，开一个二维的dp数组，第一位用二进制表示已连进的串，第二维表示以某串做结尾，这样dp数组就可以表示任何一种状态的最少字符消耗

对于转移暴力好像也可过，用了个kmp 一发WA 因为会有子串的问题，当新加入的串是结尾串的子串的时候，更新的dp数组应该是以原本的结尾串为结尾的位置。

代码如下：

#include <iostream>
#include <cmath>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <queue>
#include <stack>
#include <list>
#include <algorithm>
#include <map>
#include <set>
#define LL long long
#define Pr pair<int,int>
#define fread() freopen("in.in","r",stdin)
#define fwrite() freopen("out.out","w",stdout)

using namespace std;
const int INF = 0x3f3f3f3f;
const int msz = 10000;
const int mod = 1e9+7;
const double eps = 1e-8;

int Next[23][23];
int len[23];
char str[23][33];
int dp[(1<<10)][10];
int n;

void GetNext(int pos)
{
	int i,j;
	i = 0;
	j = Next[pos][0] = -1;
	while(i < len[pos])
	{
		while(j != -1 && str[pos][j] != str[pos][i]) j = Next[pos][j];
		++i,++j;
		Next[pos][i] = j;
	}
}

int get(int a,int b)
{
	int i,j;
	i = j = 0;
	while(i < len[a])
	{
		while(j != -1 && str[b][j] != str[a][i]) j = Next[b][j];
		++j,++i;
		if(j == len[b]) return 0;
	}
	return len[b]-j;
}

int main()
{
	//fread();
	//fwrite();

	int t;
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d",&n);
		for(int i = 0; i < n; ++i)
		{
			scanf("%s",str[i]);
			len[i] = strlen(str[i]);
		}

		memset(dp,INF,sizeof(dp));
		for(int i = 0; i < n; ++i)
		{
			GetNext(i);
			dp[1<<i][i] = len[i];
		}

		int tot = 1<<n;
		for(int i = 0; i < tot; ++i)
			for(int j = 0; j < n; ++j)
				if(i&(1<<j))
				for(int k = 0; k < n; ++k)
				{
					if(i&(1<<k)) continue;
					int tmp = get(j,k);
					if(tmp) dp[i+(1<<k)][k] = min(dp[i+(1<<k)][k],dp[i][j]+get(j,k));
					else dp[i+(1<<k)][j] = min(dp[i+(1<<k)][j],dp[i][j]);
				}

		int ans = INF;
		for(int i = 0; i < n; ++i)
			ans = min(ans,dp[tot-1][i]);
		printf("%d\n",ans);
	}

	return 0;
}

【POJ 1699】 Best Sequence（KMP+状压DP）

原文：http://blog.csdn.net/challengerrumble/article/details/50838581