前一段看了很多的红黑树的文章,终于对红黑树算是可以对红黑树有了简单的理解,一直想趁热乎写一篇自己的关于红黑树的博文,但是最近一直维护的项目突然又有了新的开发任务,今天趁着可以清闲的时间抓紧写一下,文章里面的图是我先在纸上画的,然后又用visio画了一遍,花了很长时间,不过就我目前对红黑树浅显的了解,我的介绍中可能还会有错误,欢迎纠正和分享经验。
一、下面先简单介绍一下红黑树:
红黑树是一棵接近平衡的二叉搜索树,他具备二叉搜索树的所有性质,同时由于其接近平衡所以可以保证红黑树插入、查找和删除的效率。
红黑树的五个性质:
1、每个节点要么是红色要么是黑色。
2、根节点是黑色。
3、NIL节点(空节点)是黑色。
4、如果一个节点是红色那么他的两个孩子节点都是黑色。(即同一条路径上不存在两个相邻的红色节点)。
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
由于红黑树的这些性质,可以保证红黑树的近平衡性,同时这些性质也导致了在对红黑树进行插入和删除时为了保证红黑树的特性造成了困难,在进行插入和删除之后就需要进行一些调整操作(左旋,右旋和着色)。
二、左旋和右旋。
关于左旋的示意图如下:
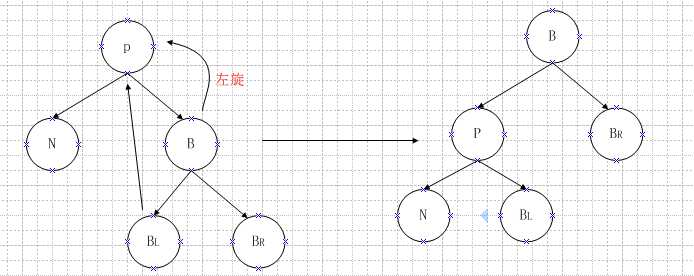
图2.1 左旋操作
这张图的左旋操作是以P为轴进行左旋操作,操作后B变为新的根结点,Br变为P的左孩子节点。
代码如下:
1 if(P->parent != NULL) 2 { 3 B->parent = P->parent; 4 if(P == P->parent->left) 5 { 6 P->parent->left = B; 7 } 8 else 9 { 10 P->parent->right = B; 11 } 12 } 13 14 B->right = P; 15 16 P->parent = B; 17 P->left = B->right; 18 19 if(B->right != NULL) 20 { 21 B->right->parent = P; 22 }
关于右旋的示意图如下:
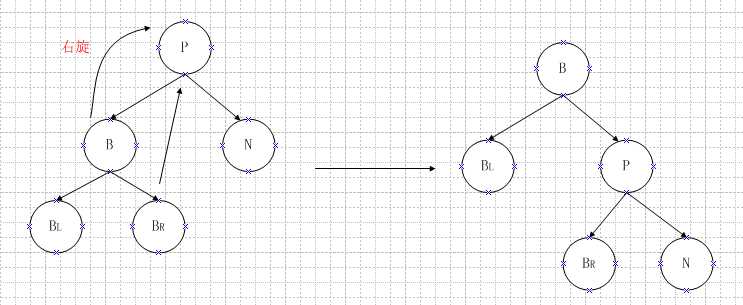
图2.1 右旋操作
由于右旋和左旋操作类似,这里就不细说了。
三、红黑树的插入
红黑树的插入主要有四种情况,下面针对这四种情况进行说明。
首先做一下统一规定,插入的节点设为N,父节点设为P,祖父节点设为G,叔叔节点设为U,并且由于插入黑节点必定会导致一中我说的红黑树性质5的破坏,所以插入节点置为红色。
3.1、插入节点的父节点P为黑色。
如下图所示
由于父节点为黑色所以插入节点后的新树已然满足红黑树的五条性质,所以不用进行调整,直接插入即可。
下面关于红黑树插入的几种情况中父节点的颜色均为红色且只考虑父节点是祖父节点的左孩子的情况,由于父节点是祖父节点的右孩子的情况和父节点是左孩子的情况对称,就不描述了。
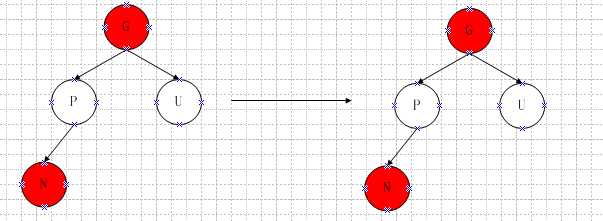
3.2、父节点和叔父节点都是红色。
做如下图所示转换
即将父节点和叔父节点置为黑色色,祖父节点置为红色。
操作代码如下
1 U->color = BLACK; 2 P->color = BLACK; 3 G->color = RED; 4 N = G;
最后由于祖父G变为了红色可能继续导致树的性质破坏,所以需要对G做为继续操作的节点。
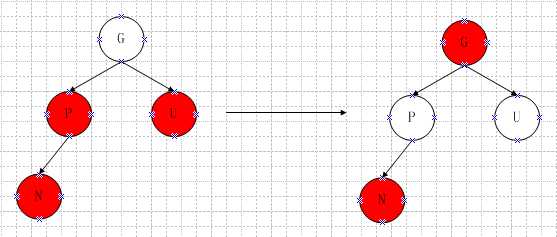
3.3、父节点红色,叔父节点黑色,且插入节点N是父节点的右孩子。
需要做如下图所示转换:
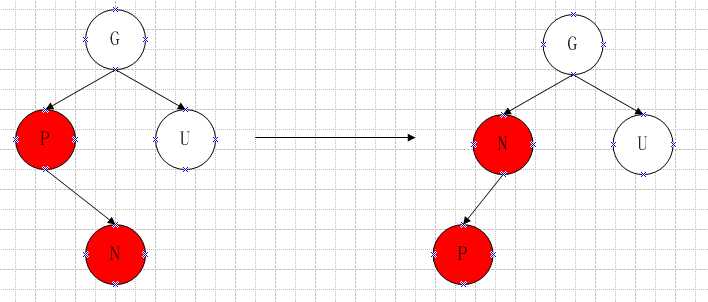
即以P为轴进行一次左旋操作。
操作代码如下:
1 rotate_left(P); 2 tmp = P; 3 P = N; 4 N = tmp;
由于左旋后N,P互换位置了,所以需要交换N,P(但是对树中不改变,只是为了继续进行修改红黑树操作时的更新N,P)。
3.4、N的叔节点U是黑色,并且N是P的左孩子。(可能由情况2变化而来的)
需要做如下图所示变换
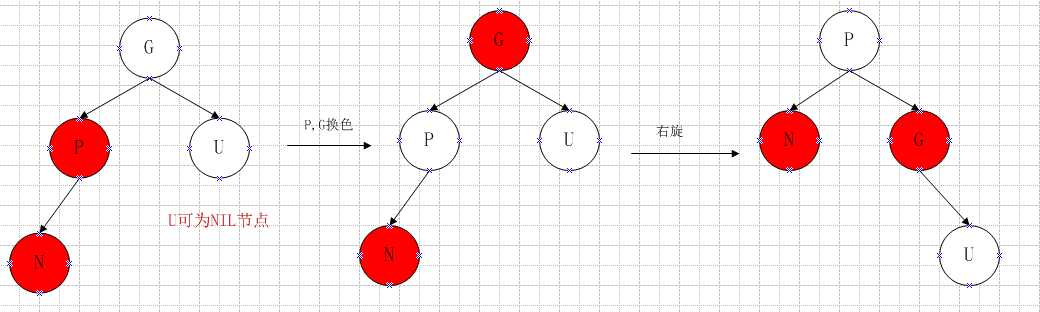
即P,G颜色互换,然后以G为轴进行一次右旋操作。
操作代码如下:
1 P->color = BLACK; 2 G->color = RED; 3 rotate_right(gparent);
由于当父节点P是祖父节点G的右孩子节点时和P是G的左孩子节点对称,同样是这三种情况,只不过旋转方向相反,所以就不描述了,至此红黑树的插入操作已经介绍完了,下面介绍红黑树的删除操作。
原文:http://www.cnblogs.com/daimadebanyungong/p/5250894.html