图论——图的基本概念,图的可行遍性
无向图:G = <V,E>, 其中 (1)V ≠ ∅为结点集,元素称为结点(顶点)。 (2)E为V&V的多重集,其元素称为无向边,简称边。
有向图:
D=<V,E>, 只需注意E是V×V的多重子集。
多重图与简单图:(1)无向图中的平行边及重数 (2)有向图中的平行边及重数(注意方向性) (3)多重图(含平行边) (4)简单图(不含平行边与环)
结点的度数(度):(1)设G=<V,E>为无向图, ∀v∈V, d(v):v的度 (2)设D=<V,E>为有向图, ∀v∈V, d+(v):v的出度;d-(v):v的入度;d(v):v的度 (3)△(G):G的最大度; δ(G):G的最小度。 (4)△+(D), δ+(D), △-(D), δ-(D), △(D), δ(D) (5)奇度结点与偶度结点
握手定理:①设G=<V,E>为任意无向图,V={v1,v2,…,vn}, |E|=m, 则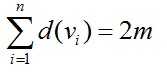
②设D=<V,E>为任意有向图,V={v1,v2,…,vn}, |E|=m, 则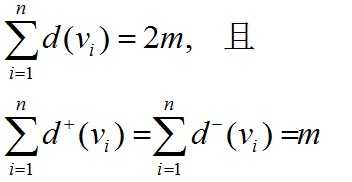
推论:任何图(无向的或有向的)中,奇度结点的个数是偶数。
定理:设非负整数列d=(d1,d2,…,dn),则d是可图化的当且仅当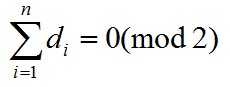
子图:G=<V,E>, G‘=<V’,E‘> (1)G’⊆G —— G‘为G的子图,G为G’的母图 (2)若G‘⊆G且V’=V,则称G‘为G的生成子图 (3)若V’⊂V或E‘⊂E,称G’为G的真子图 (4)V‘(V’⊂V且V‘≠∅)的导出子图,记作G[V’] (5)E‘(E’⊂E且E‘≠∅)的导出子图,记作G[E’]
无向图的关联矩阵:无向图G=<V,E>,|V|=n,|E|=m,令mij为vi与ej的关联次数,称(mij)n×m为G的关联矩阵,记为M(G).
欧拉通路:经过图中每条边一次且仅一次行遍所有结点的通路
欧拉回路:经过图中每条边一次且仅一次行遍所有结点的回路
欧拉图:具有欧拉回路的图
半欧拉图:具有欧拉通路而无欧拉回路的图.
定理:无向图G是欧拉图当且仅当G连通且无奇度结点。
定理:无向图G是半欧拉图当且仅当G连通且恰有两个奇度结点。若有两个奇数度结点,则它们是每条欧拉通路的端点。
哈密顿通路——经过图中所有结点一次仅一次的通路.
哈密顿回路——经过图中所有结点一次仅一次的回路.
哈密顿图——具有哈密顿回路的图.
半哈密顿图——具有哈密顿通路且无哈密顿回路的图.
平凡图是哈密顿图。
哈密顿通路是初级通路,哈密顿回路是初级回路。
环与平行边不影响哈密顿性。
哈密顿图的实质是能将图中的所有结点排在同一个圈上
存在问题:对握手定理不会应用.. 例如:
对无向简单图的判定不会应用:
(由于本章知识点较多留下了树和图的着色知识点,先把前面的再巩固)
原文:http://www.cnblogs.com/20145327gc/p/5200748.html