我们已经知道,所有的矩阵变换都是线性变换,所以齐次坐标下的平移也是线性变换。
让我们从一维平移说起。为了实现一维平移,我们需要二维变换矩阵:
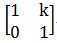
我们发现这实际上就是二维水平剪切的变换矩阵。将其效果写成向量乘法形式:
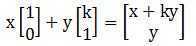
可以看出,二维剪切不改变某个点的y坐标,而将x坐标移动ky距离(x变换为x+ky)。当y=1时,x方向的平移距离就是k。这和二维剪切图形的直观效果是一致的。若将上述内容推广到更高维度,那就是N+1维的剪切在N维产生平移的效果。反过来就是,为了实现N维的平移,我们可以在N+1维对齐次坐标做剪切。
原文:http://www.cnblogs.com/byeyear/p/5149696.html