浅谈压缩感知（十五）：测量矩阵之spark常数

在压缩感知中，有一些用来评价测量矩阵的指标，如常见的RIP等，除了RIP之外，spark常数也能够用来衡量能否成为合适的测量矩阵。

1、零空间条件NULL Space Condition

在介绍spark之前，先考虑一下测量矩阵的零空间。

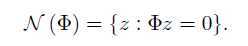
这里从矩阵的零空间来考虑测量矩阵需满足的条件：对于K稀疏的信号x，当且仅当测量矩阵的零空间与2K个基向量张成的线性空间没有交集，或者说零空间中的向量不在2K个基向量张成的线性空间中。

上述描述的性质似乎有点难懂，那么与之等价的表述就是spark常数。

2、spark常数定义

简单来说就是，矩阵列线性相关向量组的最小数目

3、spark评价定理

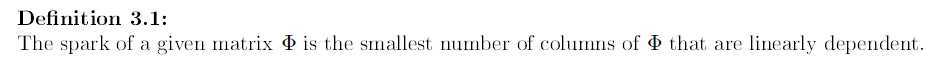
当且仅当spark(Φ)>2k时，可以通过最小0范数优化问题得到k-稀疏信号x的精确近似。

4、线性相关

定义：

定理：

性质：

5、定理证明

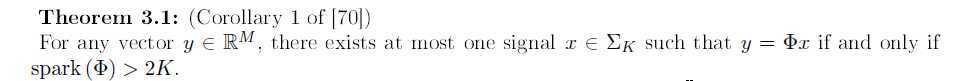
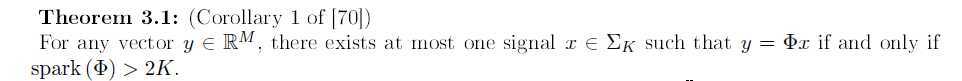
反证法。

第一步证明：对于任意的向量y，存在至多一个K稀疏的信号x，使得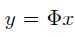，则。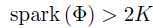

证明：假设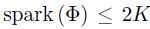，即根据定义测量矩阵的线性相关列小于或等于2K，从线性相关的定义出发，

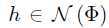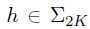存在某个向量，即，使得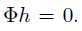且h不等于0。

由于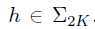，则h可以表示为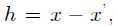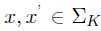：，因此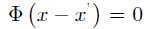

从而得到。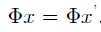

但是我们的条件中说明了至多只有一个K稀疏的信号x，因此与原条件矛盾，故假设不成立，原命题成立。

第二步证明：对于任意的向量y，满足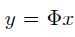且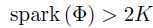的K稀疏信号x至多有一个。

证明：假设K稀疏信号x至少有两个，设为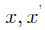，则。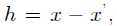

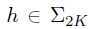因为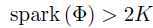，即根据定义测量矩阵的线性相关列大于2K，从线性相关的定义出发，

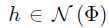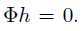存在某个向量，使得，且h不等于0。而测量矩阵的零空间应该大于2K维，而假设中的h所在子空间小于或等于2K维，要满足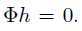，当且仅当h=0的时候，即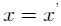，与原假设矛盾，因此假设不成立，原命题成立。

浅谈压缩感知（十五）：测量矩阵之spark常数

原文：http://www.cnblogs.com/AndyJee/p/5083726.html