Dijkstra最短路径算法是一种单源最短路径,针对的是非负权边。所谓单源最短路径就是指定一个出发顶点,计算从该源顶点出发到其他所有顶点的最短路径。
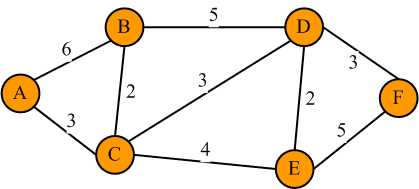
以顶点A作为出发点为例,来说明Dijkstra算法过程。
0,设置两个集合,S集合和U集合。S集合初始只有源顶点即顶点A,V集合初始为除了源顶点以外的其他所有顶点。
设置一个数组dist用来表示顶点A到其他顶点的最短距离,初始化为-1(表示无穷大)。

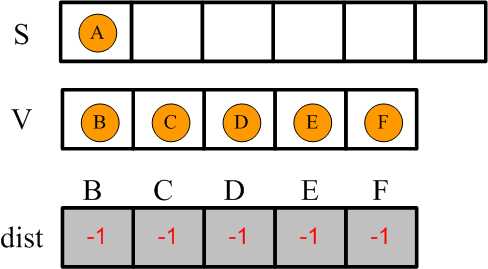
1,遍历集合V中与A直接相邻的顶点,找出当前与A距离最短的顶点。发现:
A->C = 3
A->B = 6
于是乎,将C移除集合V将其加入到集合S中,于此同时更新dist数组:
dist[C] = 3
dist[B] = 6
更新结果如下:

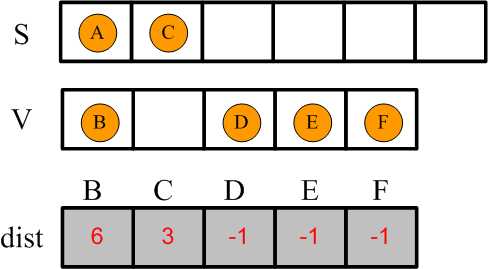
2,遍历集合V中与C相邻的顶点,发现 C->B = 2 , C->D = 3 , C->E = 4,由于目前dist中最短距离 A->C = 3 即 dist[C] = 3,那么:
A->B = 3 + 2 =5
A->D = 3 + 3 = 6
A->E = 3 + 4 = 7
而目前在dist中:
A->B = 6
A->D = -1
A->E = -1
经过比较,将顶点B加入集合S中,并将其从V集合中删除,更新dist中A->B ,A->D,A->E的记录即:
dist[B] =
5
dist[D] = 6
dist[E] = 7
更新结果如下:

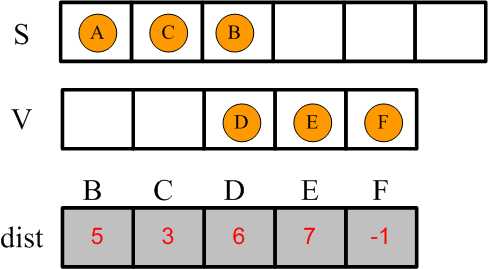
3,遍历集合V中与B相邻的顶点,发现 B->D = 5,在dist中可以查到最短距离A->B = 5, 那么:
A->D = 5 + 5 = 10
而目前在dist中:
A->D = 6
所以,将D加入到集合S中,并将其从V集合中删除,不更新dist数组相应的值,因为dist中A->D即 dist[D] 更短。更新后如下:

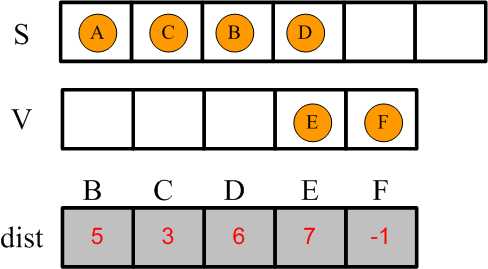
4,遍历集合V中与D相邻的顶点,发现 D->E = 2 , D->F = 3, 在dist中可以查到最短距离A->D = 6,那么:
A->E = 6 + 2 = 8
A->F = 6 + 3 = 9
而在dist中:
A->E = 7
A->F = -1
所以将E从集合V中删除并加入到集合S中,并更新dist中的:
dist[F] = 9

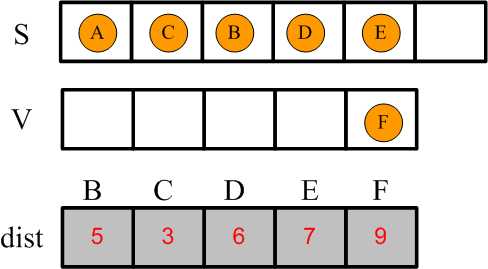
5,由于到目前为止只剩下顶点F,所以将F也加入到集合S中,至此算法运行结束。

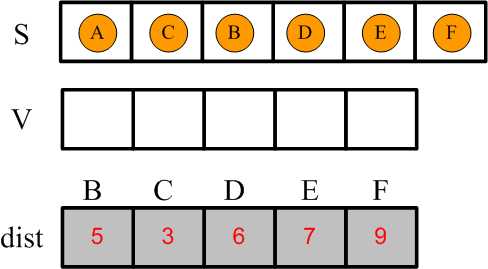
由此,dist数组就是表示从源点A出发到达其他各个顶点的最短路径,比如 A->F,dist[F] = 9。
图算法之最短路径(Dijkstra),布布扣,bubuko.com
原文:http://www.cnblogs.com/nigang/p/3658990.html