排序算法也就是我们通常说的将一组数据依照特定排序方式的一种算法。
排序算法的输出必须要遵循两个原则:
1.输出的结果为递增数列(递增针对所需的排序顺序而言)
2.输出的结果为原输入的一种排列或重组。
今天介绍的都是平均时间复杂度为O(N^2)的排序算法,即:冒泡排序、插入排序和选择排序 。
1.冒泡排序
顾名思义就是谁冒泡泡冒的快,上升的就快。 看下图:
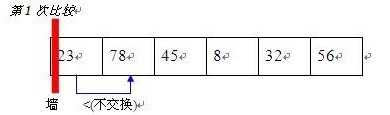
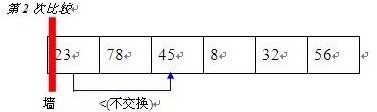
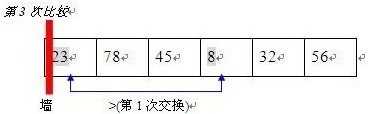
相信大家一看 就很明白,首选将两个数据进行比较,遇见比自己的大的数据,接着向后找,直到找到比自己小的数据,然后进行交换,第二个数据依次论推
上代码:
1 /*冒泡排序 复杂度O(n^2)
2 * 1.比较相邻的元素。如果第一个比第二个大,就交换他们两个。
3 2.对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
4 3.针对所有的元素重复以上的步骤,除了最后一个。
5 4.持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
6 */
7 public List<int> BubbingSort(List<int> arr)
8 {
9 int temp = 0;
10
11 for (int i = 0; i < arr.Count; i++)
12 {
13 for (int j = i + 1; j < arr.Count; j++)
14 {
15 if (arr[i] > arr[j])
16 {
17 temp = arr[i];
18 arr[i] = arr[j];
19 arr[j] = temp;
20 }
21 }
22 }
23 return arr;
24
冒泡排序最优的时间复杂度是O(n) 最差的时间复杂度O(n^2) 平均时间复杂度O(n^2)
2.插入排序
工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。时间复杂度同冒泡排序
主要有两个动作:操作和交换,如果操作的代价大于交换的代价,建议采用二分查找来减少比较操作的代价,二分查找是插入排序的一个变异算法。
直接上代码了
1 /*插入排序 默认第一个元素是已被排序
2 * 取出下一个元素 在已排序的元素中进行比较
3 * 如果已排序的元素大于该元素 则将该元素移动到下一位置
4 * 直到找到小于或等于的该元素的位置
5 * 将该元素插入到该位置
6 * 如果比较操作的代价大于交换操作的话 就要考虑用二分查找法
7 * 最差复杂度O(N^2) 最优时间复杂度O(N) 平均时间复杂度O(N^2) 空间复杂度O(N)
8 * 和冒泡排序是一个级别
9 */
10 public List<int> InsertSort(List<int> arr)
11 {
12 for (int i = 1; i < arr.Count; i++)
13 {
14 int a = arr[i];
15 int j = i;
16 while (j > 0 && arr[j - 1] > a)
17 {
18 arr[j] = arr[--j];
19 }
20 arr[j] = a;
21 }
22 return arr;
23 }
3.选择排序
在未排序序列中找到最小元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小元素,然后放到排序序列末尾(目前已被排序的序列)。以此类推,直到所有元素均排序完毕。
1 /*选择排序:首先在未排序的元素中找到最小的元素 放在排序序列的起始位置
2 然后在从生下的序列元素中继续找到最小元素,然后放在已排序序列的末尾
3 复杂度O(N^2)*/
4 public List<int> SelectSort(List<int> arr)
5 {
6 int min = 0;
7 for (int i = 0; i < arr.Count; i++)
8 {
9 min = i;
10 //查找最小值
11 for (int j = i + 1; j < arr.Count; j++)
12 {
13 if (arr[min] > arr[j])
14 min = j;
15 }
16
17 //交换
18 if (min != i)
19 {
20 int t = arr[i];
21 arr[i] = arr[min];
22 arr[min] = t;
23 }
24 }
25 return arr;
26 }
选择排序的交换操作介于0和(n-1)次之间。选择排序的比较操作为n(n-1)/2次之间。选择排序的赋值操作介于0和3(n-1)次之间。比较次数O(n^2),比较次数与关键字的初始状态无关,总的比较次数N=(n-1)+(n-2)+...+1=n*(n-1)/2。 交换次数O(n),最好情况是,已经有序,交换0次;最坏情况是,逆序,交换n-1次。 交换次数比冒泡排序少多了,由于交换所需CPU时间比比较所需的CPU时间多,n值较小时,选择排序比冒泡排序快。
原文:http://www.cnblogs.com/Drubn/p/4996574.html